题目内容
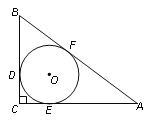
【题目】如图,点E是正方形ABCD的对角线AC上的一个动点(不与A、C重合),作EF⊥AC交边BC于点F,连接AF、BE交于点G.
(1)求证:△CAF∽△CBE;
(2)若AF平分∠BAC,求证:AC2=2AGAF.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用AA证明△CEF∽△CAB,再列出比例式利用SAS证明△CAF∽△CBE
(2)根据题意求出△ABF∽△AGB,再转化相关关系即可解答.
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵EF⊥AC,
∴∠FEC=90°=∠ABC,
又∵∠FCE=∠ACB,
∴△CEF∽△CAB,
∴![]() =
=![]() ,
,
又∵∠ACF=∠BCE,
∴△CAF∽△CBE;
(2)∵△CAF∽△CBE,
∴∠CAF=∠CBE,
∵AF平分∠BAC,
∴∠BAF=∠CAF,
∴∠BAF=∠CBE,
∴∠BAF+∠AFB=∠CBE+∠AFB=90°,
即∠ABF=∠BGA=90°,
∵∠BAG=∠BAF,
∴△ABF∽△AGB,
∴![]() =
=![]() ,
,
∴AB2=AGAF,
∵正方形ABCD中,AC2=2AB2,
∴AC2=2AGAF

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目