题目内容
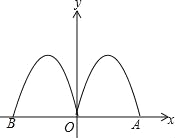
【题目】如图,抛物线y=﹣2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
A. 0<m<![]() B.
B. ![]() <m<
<m<![]()
C. 0<m<![]() D. m<
D. m<![]() 或m<
或m<![]()
【答案】A
【解析】
首先求出点A和点B的坐标,然后求出C2解析式,分别求出直线y=x+m与抛物线C1相切时m的值以及直线y=x+m过原点时m的值,结合图形即可得到答案.
令![]()
解得:x=0或x=2,
则点A(2,0),B(2,0),
∵C1与C2关于y铀对称,C1:![]()
∴C2解析式为![]()
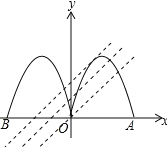
当y=x+m与C1相切时,如图所示:
令![]()
即![]()
![]()
解得![]()
当y=x+m过原点时,m=0,
∴当![]() 时直线y=x+m与C1、C2共有3个不同的交点,
时直线y=x+m与C1、C2共有3个不同的交点,
故选:A.

练习册系列答案
相关题目