题目内容
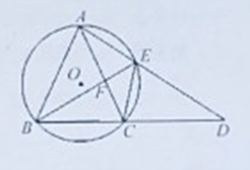
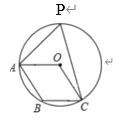
【题目】点A、B、C在⊙O上,且四边形OABC为平行四边形,P为⊙O上异于A、B、C的一点,则∠APC=___.
【答案】60°或120°
【解析】
分两种情况讨论:①当点P在优弧AC上时,由平行四边形的对角相等可知:∠AOC=∠B,然后根据圆内接四边形的对角互补可得:∠B+∠APC=180°,最后由圆周角定理和等量代换可得:∠APC+2∠APC=180°,解之即可得∠APC=60°;②当点P在劣弧AC上时,根据①可知,∠B=∠AOC=2∠APC=120°,根据同弧或等弧所对的圆周角相等可知:∠APC=∠ABC=120°.
①当点P在优弧AC上时,
∵四边形ABCO是平行四边形
∴∠AOC=∠B,
根据圆内接四边形的对角互补可知:∠B+∠APC=180°,
根据同弧所对的圆周角等于其所对的圆心角的一半可得:2∠APC=∠AOC
∴∠APC+2∠APC=180°,
解得∠APC=60°
②当点P在劣弧AC上时,
根据①可知,∠B=∠AOC=120°,
根据同弧或等弧所对的圆周角相等可知:
∠APC=∠ABC=120°,
综上所述,∠APC=60°或120°,
故答案为:60°或120°.

 文敬图书课时先锋系列答案
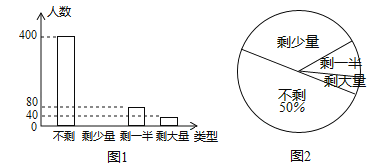
文敬图书课时先锋系列答案【题目】第二十四届冬季奧林匹克运动会将于2022年2月4日至2月20日在北京举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有![]() 名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
[收集数据]
从甲、乙两校各随机抽取![]() 名学生,在这次竞赛中他们的成绩如下:
名学生,在这次竞赛中他们的成绩如下:
甲:![]()
![]()
乙:![]()
![]()
[整理、描述数据]按如下分数段整理、描述这两组样本数据:
学校 人数 成绩 |
|
|
|
甲 |
|
|
|
乙 |
|
|
|
(说明:优秀成绩为![]() ,良好成绩为
,良好成绩为![]() 合格成绩为
合格成绩为![]() .)
.)
[分析数据]两组样本数据的平均分、中位数、众数如下表所示:
学校 | 平均分 | 中位数 | 众数 |
甲 |
|
|
|
乙 |
|
|
|
其中![]() .
.
[得出结论]
(1)小明同学说:“这次竞赛我得了![]() 分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
(2)张老师从乙校随机抽取--名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为_ ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由: ;
(至少从两个不同的角度说明推断的合理性)
【题目】某小区为改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为![]() ,并且设置了相应的垃圾箱“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为
,并且设置了相应的垃圾箱“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为![]() .
.
(1)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共![]() 吨生活垃圾,数据统计如下图(单位:吨):
吨生活垃圾,数据统计如下图(单位:吨):
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
请根据以上信息,估计“厨房垃圾”投放正确的概率;
(2)若将三类垃圾随机投入三类垃圾箱,请用画树状图或列表格的方法求出垃圾投放正确的概率.