��Ŀ����
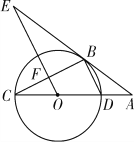
����Ŀ����6���ֹ���β˳�ν½Ӷ��������θּ�ABCDEF���������ֹܿ���ת������֪���ֹܵij���ΪAB=DE=1�ף�BC=CD=EF=FA=2�ף����½ӵ㳤�Ⱥ��Բ��ƣ�
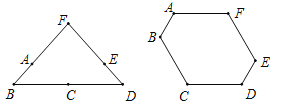
��1��ת���ֹܵõ������θּܣ���ͼ1�����A��E֮��ľ����� �ף�
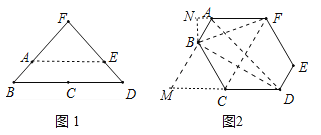
��2��ת���ֹܵõ���ͼ2��ʾ�������θּܣ��С�A=��B=��C=��D=120�㣬���������������Ӷ���ʹ�øּܲ��ܻ�����������������ܳ��ȵ���Сֵ�� �ף�
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������
�����������1����ͼ1�У���FB=DF��FA=FE�����FAE=��FEA����B=��D�����FAE=��B����AE��BD����![]() ����
����![]() ����AE=
����AE=![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��
��2����ͼ�У���BN��FA��N���ӳ�AB��DC���ڵ�M������BD��AD��BF��CF��
��RT��BFN�У��ߡ�BNF=90�㣬BN=![]() ��FN=AN+AF=
��FN=AN+AF=![]() =
=![]() ����BF=
����BF=![]() =
=![]() ��ͬ���õ�AC=DF=
��ͬ���õ�AC=DF=![]() ���ߡ�ABC=��BCD=120�㣬���MBC=��MCB=60�㣬���M=60�㣬��CM=BC=BM���ߡ�M+��MAF=180�㣬��AF��DM����AF=CM�����ı���AMCF��ƽ���ı��Σ���CF=AM=3���ߡ�BCD=��CBD+��CDB=60�㣬��CBD=��CDB�����CBD=��CDB=30�㣬�ߡ�M=60�㣬���MBD=90�㣬��BD=
���ߡ�ABC=��BCD=120�㣬���MBC=��MCB=60�㣬���M=60�㣬��CM=BC=BM���ߡ�M+��MAF=180�㣬��AF��DM����AF=CM�����ı���AMCF��ƽ���ı��Σ���CF=AM=3���ߡ�BCD=��CBD+��CDB=60�㣬��CBD=��CDB�����CBD=��CDB=30�㣬�ߡ�M=60�㣬���MBD=90�㣬��BD=![]() =
=![]() ��ͬ��BE=
��ͬ��BE=![]() ����
����![]() ��3��
��3��![]() �����������������Ӷ���ʹ�øּܲ��ܻ��������AC��BF��DF���ɣ����������������ܳ��ȵ���Сֵ
�����������������Ӷ���ʹ�øּܲ��ܻ��������AC��BF��DF���ɣ����������������ܳ��ȵ���Сֵ![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Ϊ���˽������ѧѧ��ƽ��ÿ�ܵ���������ʱ�䣬С����У�����������50��ͬѧ��ͳ�Ʋ�������Ƶ���ֲ��������±���������ͳ��ͼ����ͼ����
��� | ����ʱ�䣨h/�ܣ� | Ƶ�� |
A | 1.5��t��3 | 1 |
B | 3��t��4.5 | 2 |
C | 4.5��t��6 | a |
D | 6��t��7.5 | 20 |
E | 7.5��t��9 | 15 |
F | t��9 | b |

��1��a= �� b= ��
��2��������ͳ��ͼ�У�D����ռԲ�ĽǵĶ���Ϊ ��
��3��ȫУ����3000��ѧ�����������С�����Ƹ�Уƽ��ÿ����������ʱ�䲻����6h��ѧ��Լ�ж����ˣ�