Question

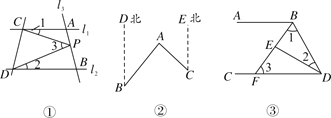
【题目】(1)如图①，已知直线l1∥l2，且l3和l1，l2分别交于A，B两点，点P在线段AB上，则∠1，∠2，∠3之间的等量关系是____；

(2)如图②，点A在B处北偏东40°方向，在C处北偏西45°方向，则∠BAC＝____°.

(3)如图③，∠ABD和∠BDC的平分线交于点E，BE交AB于点F，∠1＋∠2＝90°，试说明：AB∥AB，并探究∠2与∠3的数量关系．

Answer 1

【答案】（1）∠1＋∠2＝∠3（2）85（3）见解析，∠2＋∠3＝90°

【解析】

（1）作PM∥AC.根据平行线间的传递性，得PM∥BD.再由平行线的性质，得∠1＝∠CPM，∠2＝∠MPD.所以，∠1＋∠2＝∠3.（2）由题可知∠BAC＝∠B＋∠C，所以，∠BAC＝85°.（3）由题意，先证明AB∥AB.再通过角的变换，得到∠BED＝∠DAB＝90°，所以∠3＋∠FDE＝90，最后得到∠2＋∠3＝90.

(1)如答图，作PM∥AC，

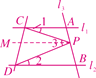
∵AC∥BD，∴PM∥BD，

∴∠1＝∠CPM，∠2＝∠MPD，

∴∠1＋∠2＝∠CPM＋∠MPD＝∠CPD＝∠3.

(2)由题可知∠BAC＝∠B＋∠C.

∵∠B＝40°，∠C＝45°，

∴∠BAC＝40°＋45°＝85°.

(3)证明：∵BE，DE分别平分∠ABD，∠BDC，

∴∠1＝∠ABD，∠2＝∠BDC.

∵∠1＋∠2＝90°，

∴∠ABD＋∠BDC＝180°，

∴AB∥AB.

∵DE平分∠BDC，

∴∠2＝∠FDE.

∵∠1＋∠2＝90°，

∴∠BED＝∠DAB＝90°，

∴∠3＋∠FDE＝90°，

∴∠2＋∠3＝90°.