题目内容
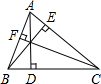如图，在三角形ABC中，AD⊥BC，BE⊥AC，CF⊥AB，BC=16，AD=3，BE=4，CF=6，你能求出三角形ABC的周长吗？
分析：利用三角形面积公式，分别解出各个边的长，再计算三角形的周长．
解答：解：由三角形面积公式可得S△ABC=
BC×AD=
AC×BE，
即16×3=4×AC，所以AC=12．
由三角形面积公式可得S△ABC=
BC×AD=
AB×CF，
即16×3=6×AB，
所以AB=8．
所以△ABC的周长为16+12+8=36．
| 1 |
| 2 |
| 1 |
| 2 |
即16×3=4×AC，所以AC=12．
由三角形面积公式可得S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即16×3=6×AB，
所以AB=8．
所以△ABC的周长为16+12+8=36．
点评：熟记三角形面积公式，本题考查了利用三角形面积公式代入数值进行计算的能力．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
43、如图，在三角形ABC中，AD是BC边上的中线，三角形ABD的周长比三角形ACD的周长小5，你能求出AC与AB的边长的差吗？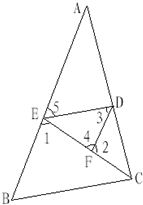
29、如图，在三角形ABC中∠1+∠2=180°，∠3=∠B以下是某同学说明∠ADE=∠ACB的推理过程或理由，请你在横线上补充完整其推理过程或理由．
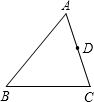如图，在三角形ABC中，AB=24，AC=18，D是AC上一点AD=12，在AB上取一点E，使A、D、E三点组成的三角形与ABC相似，则AE=
如图，在三角形ABC中，先按要求画图，再回答问题：