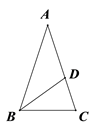题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.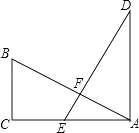
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.
【答案】
(1)解:AB=DE, AB⊥DE.
如图2,
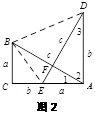
∵AD⊥CA,∴∠DAE=∠ACB=90°,
∵AE=BC,∠DAE=∠ACB,AD=AC,∴△ABC≌△DEA,∴AB=DE,
∠3=∠1,∵∠DAE=90°,∴∠1+∠2=90°,∴∠3+∠2=90°,
∴∠AFE=90°,∴AB⊥DE
(2)解:如图2,

∵S四边形ADBE= S△ADE+ S△BDE= ![]() DE·AF+
DE·AF+ ![]() DE·BF=
DE·BF= ![]() DE·AB =
DE·AB = ![]() c2,
c2,
S四边形ADBE=S△ABE+S△ADB= ![]() a2+
a2+ ![]() b2,
b2,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2,∴a2+b2=c2.
c2,∴a2+b2=c2.
【解析】(1)由题目中的已知条件可直接得到△ABC≌△DEA,问题得解;(2)四边形ADBE的两种构成:S四边形ADBE= S△ADE+ S△BDE和
S四边形ADBE=S△ABE+S△ADB,可验证勾股定理。

练习册系列答案
相关题目