题目内容
【题目】在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.
(Ⅰ)若点M的坐标为(1,﹣1),
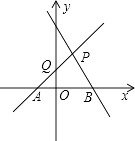
①当点F的坐标为(1,1)时,如图,求点P的坐标;
②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.
(Ⅱ)若点M(1,m),点F(1,t),其中t≠0,过点P作PQ⊥l于点Q,当OQ=PQ时,试用含t的式子表示m.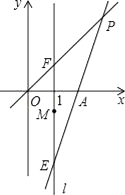
【答案】解:(Ⅰ)①∵点O(0,0),F(1,1),
∴直线OF的解析式为y=x.
设直线EA的解析式为:y=kx+b(k≠0)、
∵点E和点F关于点M(1,﹣1)对称,
∴E(1,﹣3).
又∵A(2,0),点E在直线EA上,
∴ ![]() ,
,
解得 ![]() ,
,
∴直线EA的解析式为:y=3x﹣6.
∵点P是直线OF与直线EA的交点,则 ![]() ,
,
解得 ![]() ,
,
∴点P的坐标是(3,3).
②由已知可设点F的坐标是(1,t).
∴直线OF的解析式为y=tx.
设直线EA的解析式为y=cx+d(c、d是常数,且c≠0).
由点E和点F关于点M(1,﹣1)对称,得点E(1,﹣2﹣t).
又点A、E在直线EA上,
∴ ![]() ,
,
解得 ![]() ,
,
∴直线EA的解析式为:y=(2+t)x﹣2(2+t).
∵点P为直线OF与直线EA的交点,
∴tx=(2+t)x﹣2(2+t),即t=x﹣2.
则有 y=tx=(x﹣2)x=x2﹣2x;
(Ⅱ)由(Ⅰ)可得,直线OF的解析式为y=tx.
直线EA的解析式为y=(t﹣2m)x﹣2(t﹣2m).
∵点P为直线OF与直线EA的交点,
∴tx=(t﹣2m)x﹣2(t﹣2m),
化简,得 x=2﹣ ![]() .
.
有 y=tx=2t﹣ ![]() .
.
∴点P的坐标为(2﹣ ![]() ,2t﹣
,2t﹣ ![]() ).
).
∵PQ⊥l于点Q,得点Q(1,2t﹣ ![]() ),
),

∴OQ2=1+t2(2﹣ ![]() )2,PQ2=(1﹣
)2,PQ2=(1﹣ ![]() )2,
)2,
∵OQ=PQ,
∴1+t2(2﹣ ![]() )2=(1﹣
)2=(1﹣ ![]() )2,
)2,
化简,得 t(t﹣2m)(t2﹣2mt﹣1)=0.
又∵t≠0,
∴t﹣2m=0或t2﹣2mt﹣1=0,
解得 m= ![]() 或m=
或m= ![]() .
.
则m= ![]() 或m=
或m= ![]() 即为所求.
即为所求.
【解析】(Ⅰ)①根据题意可知直线OF是正比例函数,根据点F的坐标,利用待定系数法可求出此函数的解析式;再根据点F、点M的坐标及点E和点F关于点M对称,可求出点E的坐标,利用待定系数法由点A、点E的坐标就可求得直线AE的函数解析式;再由两直线联立方程组,解方程组即可求出点P的坐标;②由已知可设点F的坐标是(1,t),设直线OF的解析式为y=tx,设直线EA的解析式为y=cx+d,再根据轴对称的性质得出点E的坐标,再将A、E的坐标代入函数解析式,即可求出直线AE的函数解析式;根据点P为直线OF与直线EA的交点,将两函数解析式联立方程组,即可求出t的值,就得到y关于x的函数解析式。
(Ⅱ)由直线OF的解析式和直线EA的解析式联立方程组,求出交点P的坐标,根据PQ⊥l于点Q,分别求出OQ2,PQ2,再根据OQ=PQ,即可求出m的值。

【题目】在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号1,2,3,4,5的五位同学最后成绩如表所示:那么这五位同学演讲成绩的众数与中位数依次是( )
参赛者编号 | 1 | 2 | 3 | 4 | 5 |
成绩/分 | 96 | 88 | 86 | 93 | 86 |
A.96,88
B.86,88
C.88,86
D.86,86