题目内容
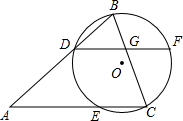 如图,⊙O的两条割线AB、AC分别交圆O于D、B、E、C,弦DF∥AC交BC于G.
如图,⊙O的两条割线AB、AC分别交圆O于D、B、E、C,弦DF∥AC交BC于G.(1)求证:AC•FG=BC•CG;
(2)若CF=AE.求证:△ABC为等腰三角形.
分析:(1)可以从探求题目的结论出发,把问题转化为证明△ABC∽△CFG,再根据图形及已知条件,找相似的条件,即两组角相等.
(2)由圆的两条平行弦CE,DF所夹的弧相等,则弦DE=CF,可证明△ADE是等腰三角形,再运用圆内接四边形的外角性质,证明△ABC是等腰三角形.
(2)由圆的两条平行弦CE,DF所夹的弧相等,则弦DE=CF,可证明△ADE是等腰三角形,再运用圆内接四边形的外角性质,证明△ABC是等腰三角形.
解答: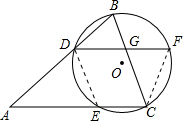 证明:(1)连接CF,
证明:(1)连接CF,
∵DF∥AC,
∴∠BDF=∠A,∠FGC=∠GCA.
∵∠BCF=∠BDF,
∴∠BCF=∠A.
∴△ABC∽△CFG(AA).
∴
=
.
∴AC•FG=BC•CG.
(2)连接DE,
∵DF∥AC,
∴DF∥EC,
∴
=
∴DE=CF.
∵CF=AE,
∴DE=AE.
∴∠A=∠ADE.
又∵∠ADE是圆内接四边形的外角,
∴∠ADE=∠ACB.
∴∠A=∠ACB.
∴△ABC是等腰三角形.
 证明:(1)连接CF,
证明:(1)连接CF,∵DF∥AC,
∴∠BDF=∠A,∠FGC=∠GCA.
∵∠BCF=∠BDF,
∴∠BCF=∠A.
∴△ABC∽△CFG(AA).
∴
| AC |
| CG |
| BC |
| FG |
∴AC•FG=BC•CG.
(2)连接DE,
∵DF∥AC,
∴DF∥EC,
∴
 |
| DE |
 |
| CF |
∴DE=CF.
∵CF=AE,
∴DE=AE.
∴∠A=∠ADE.
又∵∠ADE是圆内接四边形的外角,
∴∠ADE=∠ACB.
∴∠A=∠ACB.
∴△ABC是等腰三角形.
点评:本题综合考查圆周角定理,相似三角形的判定,等腰三角形的判定等知识点的运用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
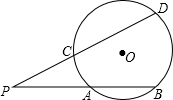 如图,⊙O的两条割线PAB,PCD分别交⊙O于点A,B和点C,D.已知PA=6,AB=4,PC=5,则CD=( )
如图,⊙O的两条割线PAB,PCD分别交⊙O于点A,B和点C,D.已知PA=6,AB=4,PC=5,则CD=( )A、
| ||
B、
| ||
| C、7 | ||
| D、24 |
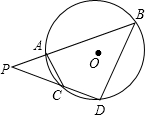 如图,⊙O的两条割线PAB和PCD分别交⊙O于点A,B和点C,D.已知PA=2,PC=4,PD=7,AC=CD,求PB,BD的长.
如图,⊙O的两条割线PAB和PCD分别交⊙O于点A,B和点C,D.已知PA=2,PC=4,PD=7,AC=CD,求PB,BD的长. 如图,⊙O的两条割线AB、AC分别交圆O于D、B、E、C,弦DF∥AC交BC于G.
如图,⊙O的两条割线AB、AC分别交圆O于D、B、E、C,弦DF∥AC交BC于G.