题目内容
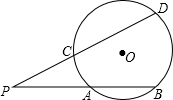如图，⊙O的两条割线PAB，PCD分别交⊙O于点A，B和点C，D．已知PA=6，AB=4，PC=5，则CD=（ ）A、
| ||
B、
| ||
| C、7 | ||
| D、24 |
分析：已知PA、AB的长，可求出PB的值，由切割线定理知PA•PB=PC•PD，即可求得PD的长，进而由CD=PD-PC求出CD的长．
解答：解：由于PAB、PCD都是⊙O的割线，根据切割线定理可得：
PA•PB=PC•PD，即PA•（PA+PB）=PC•PD，
∵PA=6，AB=4，PC=5，
∴PD=12，即CD=PD-PC=7；
故选C．
PA•PB=PC•PD，即PA•（PA+PB）=PC•PD，
∵PA=6，AB=4，PC=5，
∴PD=12，即CD=PD-PC=7；
故选C．
点评：此题主要考查的是切割线定理的应用．
练习册系列答案
相关题目
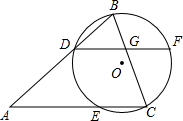如图，⊙O的两条割线AB、AC分别交圆O于D、B、E、C，弦DF∥AC交BC于G．
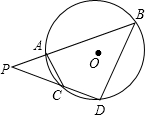如图，⊙O的两条割线PAB和PCD分别交⊙O于点A，B和点C，D．已知PA=2，PC=4，PD=7，AC=CD，求PB，BD的长．
如图，⊙O的两条割线AB、AC分别交圆O于D、B、E、C，弦DF∥AC交BC于G．