题目内容
如图,过点O作直线与双曲线y= (k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
A.S1=S2 B.2S1=S2 C.3S1=S2 D.4S1=S2
B
解析试题分析:设A点坐标为(m,n),
过点O的直线与双曲线y= 交于A、B两点,则A、B两点关与原点对称,则B的坐标为(﹣m,﹣n);
交于A、B两点,则A、B两点关与原点对称,则B的坐标为(﹣m,﹣n);
矩形OCBD中,易得OD=﹣n,OC=m;则S1=﹣mn;
在Rt△EOF中,AE=AF,故A为EF中点,
由中位线的性质可得OF=﹣2n,OE=2m;
则S2= OF×OE=﹣2mn;
OF×OE=﹣2mn;
故2S1=S2.
故选B.
考点:反比例函数系数k的几何意义

练习册系列答案
相关题目
反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )
A.y= | B.y= | C.y= | D.y= |
下列函数是反比例函数的是( )
| A.y="x" | B.y=kx﹣1 | C.y= | D.y= |
已知A(﹣1,y1),B(2,y2)两点在双曲线y=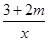 上,且 y1>y2,则m的取值范围是( )
上,且 y1>y2,则m的取值范围是( )
| A.m<0 | B.m>0 | C.m>﹣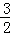 | D.m<﹣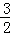 |
已知反比例函数 ,当
,当 时,
时, 随
随 的增大而增大,则关于
的增大而增大,则关于 的方程
的方程 的根的情况是( )
的根的情况是( )
| A.有两个正根 | B.有两个负根 |
| C.有一个正根一个负根 | D.没有实数根 |
若反比例函数 的图象经过点(-5,2),则
的图象经过点(-5,2),则 的值为 ( ).
的值为 ( ).
| A.10 | B.-10 | C.-7 | D.7 |

 过点A(1,0),顶点为B,且抛物线不经过第三象限。
过点A(1,0),顶点为B,且抛物线不经过第三象限。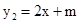 经过点B,且于该抛物线交于另一点C(
经过点B,且于该抛物线交于另一点C( ),求当x≥1时y1的取值范围。
),求当x≥1时y1的取值范围。 轴、
轴、 轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线
轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线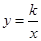 上,将正方形ABCD沿
上,将正方形ABCD沿 个单位长度后,点C恰好落在此双曲线上,则
个单位长度后,点C恰好落在此双曲线上,则