题目内容
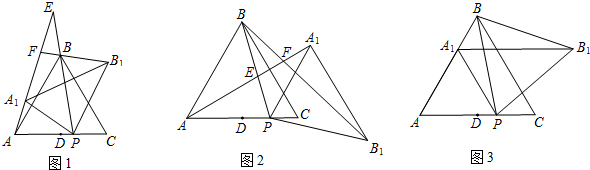
如图1，在等边△ABC中，AD是△ABC的角平分线，过点D的直线B1C1⊥AC于点C1，且交AB的延长线于点B．
（1）请你探究：
=
是否成立？
（2）请你继续探究：若△ABC为任意三角形，如图2，AD是△ABC的角平分线，请问
=
还成立吗？给出你的结论并证明．
（1）请你探究：
| AC1 |
| AB1 |
| C1D |
| DB1 |
（2）请你继续探究：若△ABC为任意三角形，如图2，AD是△ABC的角平分线，请问
| AC |
| AB |
| CD |
| DB |
分析：（1）根据等边三角形的性质得到AD垂直平分BC，∠CAD=∠BAD=30°，AB=AC，则DB=CD；由于∠C1AB1=60°，得∠B1=30°，则AB1=2AC1，同理可得到DB1=2DC1，易得
=
；
（2）过B点作BE∥AC交AD的延长线于E点，根据平行线的性质和角平分线的定义得到∠E=∠CAD=∠BAD，则BE=AB，并且根据相似三角形的判定得△EBD∽△ACD，得到
=
，而BE=AB，于是有
=
，这实际是三角形的角平分线定理．
| AC1 |
| AB1 |
| C1D |
| DB1 |
（2）过B点作BE∥AC交AD的延长线于E点，根据平行线的性质和角平分线的定义得到∠E=∠CAD=∠BAD，则BE=AB，并且根据相似三角形的判定得△EBD∽△ACD，得到
| AC |
| BE |
| CD |
| DB |
| AC |
| AB |
| CD |
| DB |
解答：解：（1）等式成立．理由如下：
∵△ABC为等边三角形，AD为角平分线，
∴AD垂直平分BC，∠CAD=∠BAD=30°，AB=AC，
∴DB=CD，
∵∠C1AB1=60°，
∴∠B1=30°，
∴AB1=2AC1，
又∵∠DAB1=30°，
∴DA=DB1，
而DA=2DC1，
∴DB1=2DC1，
∴
=
；
（2）结论仍然成立，理由如下：
如右图所示，△ABC为任意三角形，过B点作BE∥AC交AD的延长线于E点，
∴∠E=∠CAD=∠BAD，
∴BE=AB，
∵BE∥AC，
∴△EBD∽△ACD，
∴
=
，
而BE=AB，
∴
=
．
∵△ABC为等边三角形，AD为角平分线，
∴AD垂直平分BC，∠CAD=∠BAD=30°，AB=AC，
∴DB=CD，
∵∠C1AB1=60°，
∴∠B1=30°，
∴AB1=2AC1，
又∵∠DAB1=30°，
∴DA=DB1，
而DA=2DC1，
∴DB1=2DC1，
∴
| AC1 |
| AB1 |
| C1D |
| DB1 |
（2）结论仍然成立，理由如下：如右图所示，△ABC为任意三角形，过B点作BE∥AC交AD的延长线于E点，
∴∠E=∠CAD=∠BAD，
∴BE=AB，
∵BE∥AC，
∴△EBD∽△ACD，
∴
| AC |
| BE |
| CD |
| DB |
而BE=AB，
∴
| AC |
| AB |
| CD |
| DB |
点评：本题考查了相似三角形的判定与性质：平行于三角形一边的直线被其它两边所截，所截得的三角形与原三角形相似；相似三角形对应边的比相等．也考查了等边三角形的性质、含30°的直角三角形三边的关系以及角平分线的性质．
练习册系列答案
名校课堂系列答案
相关题目
