题目内容
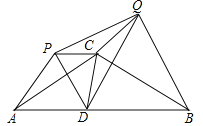
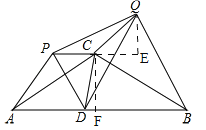
【题目】如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
①CD=CP=CQ;
②∠PCQ的大小不变;
③△PCQ面积的最小值为![]() ;
;
④当点D在AB的中点时,△PDQ是等边三角形,其中所有正确结论的序号是 .
【答案】①②④.
【解析】
试题①∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,∴CP=CD=CQ,∴①正确;
②∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,∴∠ACP=∠ACD,∠BCQ=∠BCD,∴∠ACP+∠BCQ=∠ACD+∠BCD=∠ACB=120°,∴∠PCQ=360°﹣(∠ACP+BCQ+∠ACB)=360°﹣(120°+120°)=120°,∴∠PCQ的大小不变;∴②正确;
③如图,过点Q作QE⊥PC交PC延长线于E,∵∠PCQ=120°,∴∠QCE=60°,在Rt△QCE中,tan∠QCE=![]() ,∴QE=CQ×tan∠QCE=CQ×tan60°=
,∴QE=CQ×tan∠QCE=CQ×tan60°=![]() CQ,∵CP=CD=CQ,∴S△PCQ=
CQ,∵CP=CD=CQ,∴S△PCQ=![]() CP×QE=
CP×QE=![]() CP×
CP×![]() CQ=
CQ=![]() ,∴CD最短时,S△PCQ最小,即:CD⊥AB时,CD最短,过点C作CF⊥AB,此时CF就是最短的CD,∵AC=BC=4,∠ACB=120°,∴∠ABC=30°,∴CF=
,∴CD最短时,S△PCQ最小,即:CD⊥AB时,CD最短,过点C作CF⊥AB,此时CF就是最短的CD,∵AC=BC=4,∠ACB=120°,∴∠ABC=30°,∴CF=![]() BC=2,即:CD最短为2,∴S△PCQ最小=
BC=2,即:CD最短为2,∴S△PCQ最小=![]() =
=![]() =
=![]() ,∴③错误;
,∴③错误;
④∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,∴AD=AP,∠DAC=∠PAC,∵∠DAC=30°,∴∠APD=60°,∴△APD是等边三角形,∴PD=AD,∠ADP=60°,同理:△BDQ是等边三角形,∴DQ=BD,∠BDQ=60°,∴∠PDQ=60°,∵当点D在AB的中点,∴AD=BD,∴PD=DQ,∴△DPQ是等边三角形,∴④正确,故答案为:①②④.