Question

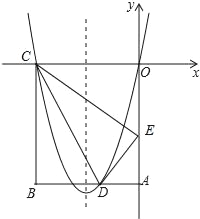
【题目】如图，已知点A（0，2），B（2，2），C（-1，-2），抛物线F：y=x2-2mx+m2-2与直线x=-2交于点P．

（1）当抛物线F经过点C时，求它的解析式；

（2）设点P的纵坐标为yP，求yP的最小值，此时抛物线F上有两点（x1，y1），（x2，y2），且x1＜x2≤-2，比较y1与y2的大小.

Answer 1

【答案】(1) ；(2).

【解析】

（1）根据抛物线F：y=x2-2mx+m2-2过点C（-1，-2），可以求得抛物线F的表达式；
（2）根据题意，可以求得yP的最小值和此时抛物线的表达式，从而可以比较y1与y2的大小.

(1) ∵抛物线F经过点C（－1，－2），

∴.

∴m1=m2=-1.

∴抛物线F的解析式是.

(2)当x=-2时，=.

∴当m=-2时，的最小值为－2.

此时抛物线F的表达式是.

∴当时，y随x的增大而减小.　

∵≤－2，

∴>.