Question

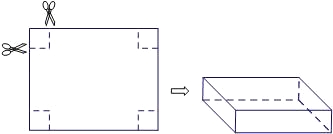
【题目】如图，把一张长15cm，宽12cm的矩形硬纸板的四周各剪去一个同样大小的小正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）．设剪去的小正方形的边长为xcm．

（1）请用含x的代数式表示长方体盒子的底面积；

（2）当剪去的小正方形的边长为多少时，其底面积是130cm2？

（3）试判断折合而成的长方体盒子的侧面积是否有最大值？若有，试求出最大值和此时剪去的小正方形的边长；若没有，试说明理由．

Answer 1

【答案】（1）（15﹣2x）（12﹣2x）cm2；（2）当剪去的小正方形的边长为cm时，长方体盒子的侧面积有最大值．

【解析】

试题分析：（1）由图可知：长方体盒子的底面的长和宽分别是原矩形的长和宽减去两个小正方形的边长，根据矩形的面积=长×宽；

（2）得出一个关于正方形边长x的方程．从而求解；

（2）长方体盒子的侧面积是四个小矩形，都是以正方形的边长为宽，以盒子的底面的长或宽为长，根据这个关系，我们可列出关于侧面积和正方形边长x的函数关系式，然后根据函数的性质来求出这个最值．

试题解析：（1）（15﹣2x）（12﹣2x）cm2；

（2）依题意得：（15﹣2x）（12﹣2x）=130，即2x2﹣27x+25=0，

解得x1=1，（不合题意，舍去），

∴当剪去的小正方形的边长为1cm时，其底面积是130cm2；

（3）设长方体盒子的侧面积是S，则S=2[（15﹣2x）x+（12﹣2x）x]，即S=54x﹣8x2，

S=﹣8（x﹣）2+，（0＜x＜6），当x=时，，

即当剪去的小正方形的边长为cm时，长方体盒子的侧面积有最大值．