Question

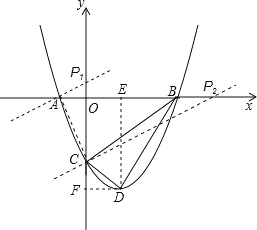
【题目】如图，抛物线与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C（0，﹣3），设抛物线的顶点为D．

（1）求该抛物线的解析式与顶点D的坐标；

（2）以B、C、D为顶点的三角形是直角三角形吗？为什么？

（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCD相似？若存在，请指出符合条件的点P的位置，并直接写出点P的坐标；若不存在，请说明理由．

Answer 1

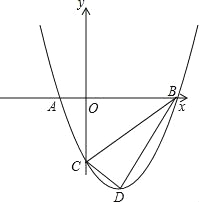
【答案】（1）顶点D的坐标为（1，﹣4）．（2）△BCD为直角三角形．（3）符合条件的点有三个：O（0，0），，P2（9，0）．

【解析】

试题分析：（1）已知了抛物线图象上的三点坐标，可用待定系数法求出该抛物线的解析式，进而可用配方法或公式法求得顶点D的坐标．

（2）根据B、C、D的坐标，可求得△BCD三边的长，然后判断这三条边的长是否符合勾股定理即可．

（3）假设存在符合条件的P点；首先连接AC，根据A、C的坐标及（2）题所得△BDC三边的比例关系，即可判断出点O符合P点的要求，因此以P、A、C为顶点的三角形也必与△COA相似，那么分别过A、C作线段AC的垂线，这两条垂线与坐标轴的交点也符合点P点要求，可根据相似三角形的性质（或射影定理）求得OP的长，也就得到了点P的坐标．

试题解析：（1）设该抛物线的解析式为y=ax2+bx+c，

由抛物线与y轴交于点C（0，﹣3），可知c=﹣3，

即抛物线的解析式为y=ax2+bx﹣3，

把A（﹣1，0）、B（3，0）代入，

得

解得a=1，b=﹣2．

∴抛物线的解析式为y=x2﹣2x﹣3，

∴顶点D的坐标为（1，﹣4）．

（2）以B、C、D为顶点的三角形是直角三角形，

理由如下：

过点D分别作x轴、y轴的垂线，垂足分别为E、F．

在Rt△BOC中，OB=3，OC=3，

∴BC2=18，

在Rt△CDF中，DF=1，CF=OF﹣OC=4﹣3=1，

∴CD2=2，

在Rt△BDE中，DE=4，BE=OB﹣OE=3﹣1=2，

∴BD2=20，

∴BC2+CD2=BD2，故△BCD为直角三角形．

（3）连接AC，则容易得出△COA∽△CAP，又△PCA∽△BCD，可知Rt△COA∽Rt△BCD，得符合条件的点为O（0，0）．

过A作AP1⊥AC交y轴正半轴于P1，可知Rt△CAP1∽Rt△COA∽Rt△BCD，

求得符合条件的点为．

过C作CP2⊥AC交x轴正半轴于P2，可知Rt△P2CA∽Rt△COA∽Rt△BCD，

求得符合条件的点为P2（9，0）．

∴符合条件的点有三个：O（0，0），，P2（9，0）．