题目内容
【题目】已知:如图①,在△ABC中,BC=AC,在△CDE中,CE=CD,现把两个三角形的C点重合,且使∠BCA=∠ECD,连接BE、AD.
(1)求证:BE=AD
(2)若将△ECD绕点C旋转至图②、③所示的情况时,其余条件不变,BE与AD还相等么?若相等,请给与证明;若不相等,请说明理由.

【答案】(1)见解析;(2)BE与AD相等,理由见解析.
【解析】
(1)由∠BCA=∠ECD可推出∠BCE=∠ACD,然后利用SAS即可证明△BCE≌△ACD,从而得到BE=AD;
(2)图②可直接利用SAS即可证明△BCE≌△ACD,从而得到BE=AD;图③先由∠BCA=∠ECD推出∠BCE=∠ACD,然后利用SAS即可证明△BCE≌△ACD,从而得到BE=AD.
证明:(1)∵∠BCA=∠ECD
∴∠BCA-∠ECA=∠ECD-∠ECA
即∠BCE=∠ACD
在△BCE和△ACD中,
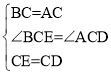
∴△BCE≌△ACD(SAS)
∴BE=AD
(2)BE与AD相等,理由如下:
如图②,在△BCE和△ACD中,
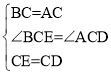
∴△BCE≌△ACD(SAS)
∴BE=AD
如图③,∵∠BCA=∠ECD
∴∠BCA+∠ACE=∠ECD+∠ACE
即∠BCE=∠ACD,
在△BCE和△ACD中,
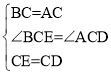
∴△BCE≌△ACD(SAS)
∴BE=AD

练习册系列答案
相关题目




