题目内容
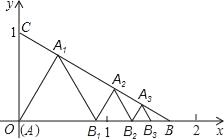
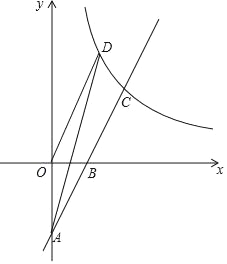
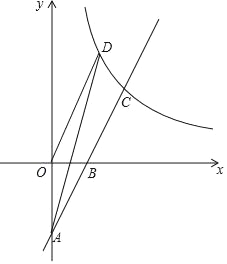
【题目】如图,在平面直角坐标系中,直线y=kx﹣4(k≠0)与坐标轴交于A、B两点,与反比例函数y=![]() (m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=
(m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=![]() .
.
(1)求一次函数和反比例函数的解析式.
(2)求△AOD的面积.
【答案】(1)y=2x﹣4,y=![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据y=kx﹣4(k≠0)求得A(0,﹣4),即可得OA=2;在Rt△ABO中根据锐角三角函数的定义求得OB=2,即可得B(2,0),将B(2,0)代入y=kx﹣4(k≠0)中求得k=2,再求得C(4,4),代入求得反比例函数的解析式即可;(2)求得点D的坐标,根据三角形的面积公式即可求解.
试题解析:
(1)在y=kx﹣4(k≠0)中,当x=0时y=﹣1,
∴A(0,﹣4),
在Rt△ABO中:tan∠OAB=![]() =
=![]() ,
,
∴OB=2,
∴B(2,0),
将B(2,0)代入y=kx﹣4(k≠0)中:k=2,
∴y=2x﹣4,
当x=4时,y=4,
∴C(4,4),
∴m=4×4=16,
∴y=![]() ;
;
(2)当y=6时,x=![]() ,
,
∴D(![]() ,6),
,6),
∴S=![]() ×4×
×4×![]() =
=![]() .
.

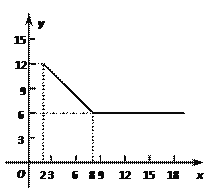
【题目】我国是水资源比较贫乏的国家之一,为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段来达到节约用水的目的,规定如下用水收费标准:每户每月的用水不超过20立方米(含20立方米)时,水费按“基本价”收费:超过20立方米时,不超过的部分仍按“基本价”收费,超过部分按“调节价”收费.某户居民今年4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
4 | 20 | 42 |
5 | 24 | 56.40 |
(1)请你算一算该市水费的“调节价”每立方米多少元?
(2)若该户居民6月份用水量为30立方米,请算一算,6月份水费是多少元?
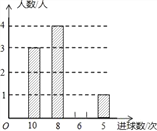
【题目】某校九年级学生在一节体育课中,选一组学生进行投篮比赛,每人投10次,汇总投进球数的情况进行统计分析,绘制了如下不完整的统计表和统计图.
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中选一名学生参加校动会投篮比赛,投进10球的成员被选中的概率为多少?