题目内容
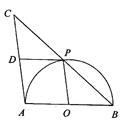
【题目】如图，AB是半圆O的直径，点P是半圆上不与点A，B重合的一个动点，延长BP到点C，使PC＝PB，D是AC的中点，连接PD，PO．
（1）求证：△CDP≌△POB；
（2）填空：
①若AB＝4，则四边形AOPD的最大面积为_______，此时BD=_______；
②连接OD，当∠PBA的度数为________时，四边形BPDO是菱形．
【答案】（1）见解析；（2）①4，
；②60°
【解析】
（1）根据中位线的性质得到DP∥AB，DP=
AB，由SAS可证△CDP≌△POB；
（2）①当四边形AOPD的AO边上的高等于半径时有最大面积，依此即可求得BD；
②根据有一组对应边平行且相等的四边形是平行四边形，可得四边形BPDO是平行四边形，再根据邻边相等的平行四边形是菱形，以及等边三角形的判定和性质即可求解．
(1)证明：∵PC=PB，D是AC的中点，
∴DP∥AB，
∴DP=AB，∠CPD=∠PBO，
∵BO=AB，
∴DP=BO，
在△CDP与△POB中，
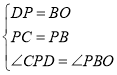
∴△CDP≌△POB(SAS)；
(2)①当四边形AOPD的AO边上的高等于半径时有最大面积，
(4÷2)×(4÷2)
=2×2
=4；
BD=
=
②如图：
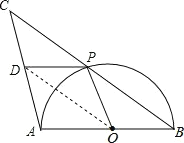
∵DP∥AB，DP=BO，
∴四边形BPDO是平行四边形，
∵四边形BPDO是菱形，
∴PB=BO，
∵PO=BO，
∴PB=BO=PO，
∴△PBO是等边三角形，
∴∠PBA的度数为60°.
练习册系列答案
相关题目
