题目内容
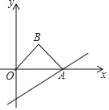
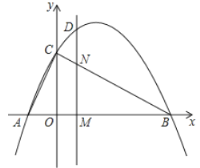
【题目】二次函数![]() 的图象交x轴于A(-1, 0),B(4, 0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC.设运动的时间为t秒.
的图象交x轴于A(-1, 0),B(4, 0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC.设运动的时间为t秒.
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接BD,当![]() 时,求△DNB的面积;
时,求△DNB的面积;
(3)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,直接写出此时点D的坐标.
【答案】(1)![]() ;(2)2;(3)(1,0)或(3,0) D(1,3)或(3,2)
;(2)2;(3)(1,0)或(3,0) D(1,3)或(3,2)
【解析】
(1)将A、B的坐标代入解答即可.
(2)先求出BC的解析式![]() ,再将x=2代入
,再将x=2代入![]() 和
和![]() ,得出D、N的坐标即可求出DN的值,再根据三角形的面积公式计算出答案即可.
,得出D、N的坐标即可求出DN的值,再根据三角形的面积公式计算出答案即可.
(3)由BM的值得出M的坐标![]() ,设P(2t-1,m),由勾股定理可得
,设P(2t-1,m),由勾股定理可得![]() ,根据题意PB=PC,所以
,根据题意PB=PC,所以![]() ,得出P的坐标为
,得出P的坐标为![]() ,PC⊥PB故
,PC⊥PB故![]() ,解得t=1或t=2,即得出答案.
,解得t=1或t=2,即得出答案.
(1)将A(-1, 0),B(4, 0)代入![]() 中,得:
中,得:
![]()
解得: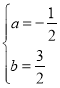
故二次函数的表达式为:![]()
(2)![]()
![]() AM=3
AM=3
又![]()
![]()
设BC的表达式为![]()
将点C(0,2),B(4,0)代入得:
![]()
解得: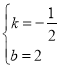
故直线BC的解析式为:![]()
将x=2代入![]() 和
和![]() ,
,
得D(2,3),N(2,1)
![]()
![]()
![]()
(3)![]()
![]()
设P(2t-1,m)
![]()
![]() ,且PB=PC
,且PB=PC
![]()
![]()
![]()
![]() PC⊥PB
PC⊥PB
![]()
![]() t=1或t=2
t=1或t=2
![]() 或者
或者![]()
![]() D(1,3)或者D(3,2)
D(1,3)或者D(3,2)

【题目】某健身器材公司销售A,B两款跑步机,这两款跑步机的进价和售价如下表所示:
| A | B |
进价 | 4500 | 6200 |
售价 | 6000 | 8000 |
该公司计划购进两款跑步机若干台,共需![]() 万元,全部销售后可获利
万元,全部销售后可获利![]() 万元.
万元.
![]() 问该公司计划购进A,B两款跑步机各多少台?
问该公司计划购进A,B两款跑步机各多少台?
![]() 为了适应市场需求的变化,该公司决定在原计划的基础上,减少A款跑步机的购进数量,增加B款跑步机的购进数量,已知B款跑步机增加的数量是A款跑步机减少的数量的2倍.若用于购进这两种款跑步机的总资金不超过29.6万元,问A种款跑步机购进数量至多减少多少台?
为了适应市场需求的变化,该公司决定在原计划的基础上,减少A款跑步机的购进数量,增加B款跑步机的购进数量,已知B款跑步机增加的数量是A款跑步机减少的数量的2倍.若用于购进这两种款跑步机的总资金不超过29.6万元,问A种款跑步机购进数量至多减少多少台?