Question

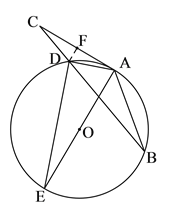
【题目】如图，在△ABC中，点D为BC上一点，过A，B，D三点作⊙O，AE是⊙O的直径，AC是⊙O的切线，AD=DC，连结DE．

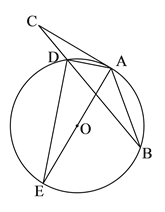
（1）求证：AB=AC；

（2）若，AC=，求△ADE的周长.

Answer 1

【答案】（1）证明见解析;（2）12+.

【解析】（1）证明：∵AD=DC，∴∠CAD=∠C.

∵AC是⊙O的切线，∴∠CAE=90°.

∴∠CAD+∠EAD=90°.

∵AE是⊙O的直径，∴∠ADE=90°.

∴∠E+∠EAD=90°.∴∠CAD=∠E.

又∵∠E=∠B，∴∠C=∠B.

∴AB=AC.

（2）解：过点D作DF⊥AC于点F.

①由DA=DC，AC=，可得CF= =.

②由∠C=∠E， ，可得.在 Rt△CDF中，求出CD=DA=3

(或利用△CDF∽△ADE求).

③在 Rt△ADE中，利用，求出AE=9.

再利用勾股定理得出DE=

④△ADE的三边相加得出周长为12+.