题目内容
【题目】如图,在等边三角形ABC中,AE=CD,AD、BE交于Q点,BP⊥AD于P点. 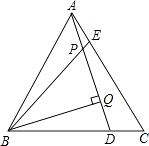
求证:
(1)△BAE≌△ACD;
(2)∠BQP=60°;
(3)BQ=2PQ.
【答案】
(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
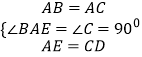 ,
,
∴△ABE≌△CAD(SAS)
(2)∵△ABE≌△CAD
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°
(3)∵BQ⊥AD,
∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,
∴BP=2PQ.
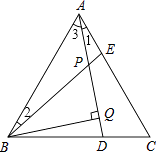
【解析】(1)由AB=AC,∠BAE=∠C,AE=CD,即可证明.(2)根据三角形的外角的性质,∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,即可证明.(3)利用直角三角形30度性质即可解决问题.
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】某校组织数学学科竞赛为参加区级比赛做选手选拔工作,经过多次测试后,有四位同学成为晋级的候选人,具体情况如下表,如果从这四位同学中选出一名晋级(总体水平高且状态稳定)你会推荐( )
甲 | 乙 | 丙 | 丁 | |
平均分 | 92 | 94 | 94 | 92 |
方差 | 35 | 35 | 23 | 23 |
A. 甲 B. 乙 C. 丙 D. 丁