题目内容
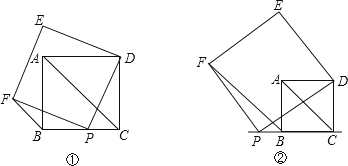
【题目】如图①,点P是正方形ABCD的BC边上的一点,以DP为边长的正方形DEFP与正方形ABCD在BC的同侧,连接AC、FB.
(1)请你判断FB与AC又怎样的位置关系?并证明你的结论;
(2)若点P在射线CB上运动时,如图②,判断(1)中的结论FB与AC的位置关系是否仍然成立?并说明理由;
(3)当点P在直线CB上运动时,请你指出点E的运动路线,不必说明理由.
【答案】(1)FB∥AC,证明见解析;
(2)结论仍成立,理由见解析;
(3)当点P在直线BC上移动时,E的轨迹是图中的线段GA.
【解析】分析:(1)过F作FM⊥BC于M,证△PFM≌△DPC(AAS),推出DC=PM,FM=PC,求出∠FBM=45°即可.(2)中结论是还正确,过F作FM⊥BC于M,证△PFM≌△DPC(AAS),推出DC=PM,FM=PC,求出∠FBM=45°即可.(3)当点P在直线BC上移动时,E的轨迹是图中的线段GA,理由是△DCP绕D顺时针旋转90°,到达△DAE 即可以确定E的轨迹.
本题解析:(1)FB∥AC,
证明:过F作FM⊥BC于M,∵四边形ABCD、DEFP是正方形,∴∠ACB=45°,DC=BC,PF=DP,∠DCP=∠M=∠FPD=90°,
∴∠MFP+∠FPM=∠FPM+∠DPC=90°,∴∠MFP=∠CPD,
在△PFM和△DPC中:∠MFP=∠DPC,∠M=∠DCP, PF=DP
∴△PFM≌△DPC(AAS),∵DC=PM,FM=PC,∵DC=BC,
∴BC=DC=PM,∴PM-BP=BC-BP,∴BM=CP,∵FM=CP,∴FM=BM,∵∠M=90°,
∴∠FBM=∠MFB=0.5(180°-90°)=45°,∵∠ACB=45°,∴∠ACB=∠FBM,
∴FB∥AC;
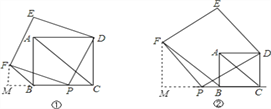
(2)结论仍成立,
理由是:过F作FM⊥BC于M,
∵四边形ABCD、DEFP是正方形,∴∠ACB=45°,DC=BC,PF=DP,∠DCP=∠M=∠FPD=90°,
∴∠MFP+∠FPM=∠FPM+∠DPC=90°,∴∠MFP=∠CPD,
在△PFM和△DPC中,
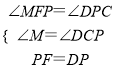 ,∴△PFM≌△DPC(AAS),
,∴△PFM≌△DPC(AAS),
∵DC=PM,FM=PC,∵DC=BC,∴BC=DC=PM,∴PM+BP=BC+BP,
∴BM=CP,∵FM=CP,∴FM=BM,∵∠M=90°,
∴∠FBM=∠MFB=0.5(180°-90°)=45°,∵∠ACB=45°,∴∠ACB=∠FBM,
∴FB∥AC;
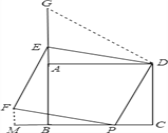
(3)当点P在直线BC上移动时,E的轨迹是图中的线段GA.

 天天练口算系列答案
天天练口算系列答案