题目内容
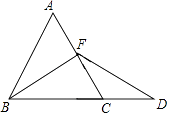
【题目】如图,已知△ABC中,高为AD,角平分线为AE,若∠B=28°,∠ACD=52°,求∠EAD的度数. 
【答案】解:在△ABC中,∵∠ACD=∠B+∠BAC,
∴∠BAC=52°﹣28°=24°,
∵AE平分∠BAC,
∴∠BAE= ![]() ∠BAC=12°,
∠BAC=12°,
∴∠AED=∠B+∠BAE=28°+12°=40°,
∵AD为高,
∴∠ADE=90°,
∴∠EAD=90°﹣∠AED=90°﹣40°=50°
【解析】先根据三角形外角性质计算出∠BAC=24°,再根据角角平分线定义得到∠BAE= ![]() ∠BAC=12°,接着再利用三角形外角性质得到∠AED=∠B+∠BAE=40°,然后根据互余计算出∠EAD的度数.
∠BAC=12°,接着再利用三角形外角性质得到∠AED=∠B+∠BAE=40°,然后根据互余计算出∠EAD的度数.
【考点精析】根据题目的已知条件,利用三角形的内角和外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目