题目内容
如图,A(-1,0)、B(2,-3)两点在一次函数y2=-x+m与二次函数y1=ax2+bx-3图像上。
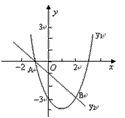
(1)求m的值和二次函数的解析式。
(2)请直接写出使y2> y1时,自变量x的取值范围。
(3)说出所求的抛物线y1=ax2+bx-3可由抛物线y=x2如何平移得到?
(2)请直接写出使y2> y1时,自变量x的取值范围。
(3)说出所求的抛物线y1=ax2+bx-3可由抛物线y=x2如何平移得到?
解:(1)把A(-1,0)代入y2=-x+m得:0=-(-1)+m,
∴m= -1。
把A(-1,0)、B(2,-3)两点代入y1=ax2+bx-3得: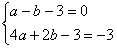 ,
,
解得: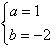 ,
,
∴y1=x2 -2x-3;
(2)当y2> y1时,-1< x<3;
(3)所求的抛物线y1=x2 -2x-3=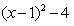 可由抛物线向上平移4个单位,再向右平移1个单位而得到。
可由抛物线向上平移4个单位,再向右平移1个单位而得到。
∴m= -1。
把A(-1,0)、B(2,-3)两点代入y1=ax2+bx-3得:
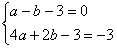 ,
,解得:
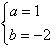 ,
,∴y1=x2 -2x-3;
(2)当y2> y1时,-1< x<3;
(3)所求的抛物线y1=x2 -2x-3=
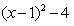 可由抛物线向上平移4个单位,再向右平移1个单位而得到。
可由抛物线向上平移4个单位,再向右平移1个单位而得到。 
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.