题目内容
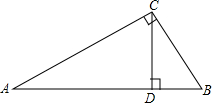 (1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=
(1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=4
4
.(2)在△ABC中,AB=15,AC=13,BC边上的高AD=12,试求△ABC的周长.
分析:(1)根据图形可得△BDC∽△CDA,从而利用对应边成比例可得出CD的长度;
(2)分情况讨论,如图所示:利用勾股定理分别求出AD、CD的长度,从而得出BC的长度,继而可得出△ABC的周长.
(2)分情况讨论,如图所示:利用勾股定理分别求出AD、CD的长度,从而得出BC的长度,继而可得出△ABC的周长.
解答: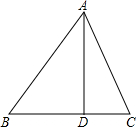 解:(1)∵∠BCD+∠ACD=90°,∠CAD+∠ACD=90°,
解:(1)∵∠BCD+∠ACD=90°,∠CAD+∠ACD=90°,
∴∠CAD=∠BCD,
∴△BDC∽△CDA,
故可得:
=
,即CD2=AD•BD=16,
∴CD=4;
(2)①在RT△ABD中,BD=
=9,在RT△ADC中,CD=
=5,
 故BC=BD+CD=14,
故BC=BD+CD=14,
从而可得△ABC的周长为42.
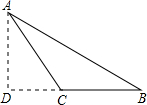
②在RT△ABD中,BD=
=9,在RT△ADC中,CD=
=5,
故BC=BD-CD=4,
从而可得△ABC的周长为32.
 解:(1)∵∠BCD+∠ACD=90°,∠CAD+∠ACD=90°,
解:(1)∵∠BCD+∠ACD=90°,∠CAD+∠ACD=90°,∴∠CAD=∠BCD,
∴△BDC∽△CDA,
故可得:
| CD |
| AD |
| BD |
| CD |
∴CD=4;
(2)①在RT△ABD中,BD=
| AC2-AD2 |
| AC2-AD2 |
 故BC=BD+CD=14,
故BC=BD+CD=14,从而可得△ABC的周长为42.
②在RT△ABD中,BD=
| AC2-AD2 |
| AC2-AD2 |
故BC=BD-CD=4,
从而可得△ABC的周长为32.
点评:此题考查了勾股定理及相似三角形的判定与性质,求解第二问的关键是利用勾股定理分别求出BD和CD,注意不要漏解.

练习册系列答案
相关题目
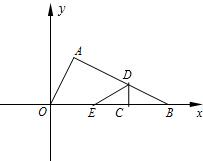 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程 如图在Rt△ABC中,∠ACB=90°,sinA=
如图在Rt△ABC中,∠ACB=90°,sinA=
 (2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6. 如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是
如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是