题目内容
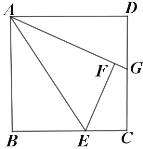
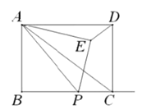
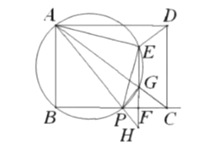
【题目】如图,在矩形![]() 中
中![]() ,
,![]() ,连结
,连结![]() ,点
,点![]() 在射线
在射线![]() 上,以
上,以![]() 为边在
为边在![]() 上方作
上方作![]() ,作
,作![]() ,连结
,连结![]() .
.
(1)当点![]() 在线段
在线段![]() 上时,证明:
上时,证明:![]() ;
;
(2)若![]() 时,求
时,求![]() 的面积;
的面积;
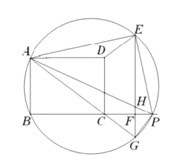
(3)![]() 的外接圆交射线
的外接圆交射线![]() 于点
于点![]() ,作直线
,作直线![]() 交直线
交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据相似三角形的判定和性质证明结论即可;
(2)分2种情况①当点![]() 在射线
在射线![]() 上时.先根据勾股定理求出AC的长,再作
上时.先根据勾股定理求出AC的长,再作![]() 于点
于点![]() ,构造直角三角形,根据相似三角形的判定和性质得出△PCM∽△ACB,进而推出
,构造直角三角形,根据相似三角形的判定和性质得出△PCM∽△ACB,进而推出![]() ,可设
,可设![]() ,
,![]() ,
,![]() ,在
,在![]() 中,由
中,由![]() ,得出PM的值,进而求得
,得出PM的值,进而求得![]() 的面积;②当点
的面积;②当点![]() 在线段
在线段![]() 上时,作
上时,作![]() 于点
于点![]() ,可得△PCM∽△ACB,同理可得
,可得△PCM∽△ACB,同理可得![]() 的面积;
的面积;
(3)分2种情况,①当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于点
于点![]() ,易得ΔEDM∽ΔGCF,设设
,易得ΔEDM∽ΔGCF,设设![]() ,求出PB的长,再由△ABP∽△HFP,根据相似三角形的性质推出
,求出PB的长,再由△ABP∽△HFP,根据相似三角形的性质推出![]() ,求出FH的长;②当点
,求出FH的长;②当点![]() 在线段
在线段![]() 上,同理可得
上,同理可得![]() .
.
(1)证明:∵在矩形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴△AEP∽△ADC,
∴![]()
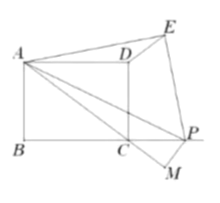
(2)①当点![]() 在射线
在射线![]() 上时.
上时.
∵![]() ,
,
∴![]() ,
,
∴![]()
![]() 中,
中,![]()
作![]() 于点
于点![]() ,
,
可得△PCM∽△ACB,
∴![]() ,
,
∴可设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() 中,
中,![]() ,
,
![]() ,
,
∴![]()
![]() 的面积
的面积![]()
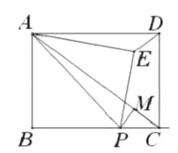
②当点![]() 在线段
在线段![]() 上时,作
上时,作![]() 于点
于点![]() ,可得△PCM∽△ACB,
,可得△PCM∽△ACB,
∴![]() ,
,
∴可设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() 中,
中,![]() ,
,
![]() ,
,
∴![]()
![]() 的面积
的面积![]()
(3)∵![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
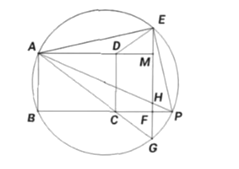
①当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于点
于点![]() ,
,
则![]() ,易得ΔEDM∽ΔGCF,
,易得ΔEDM∽ΔGCF,
设![]() ,则有
,则有![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,![]()
又∵![]() ,
,
∴△ABP∽△HFP,
∴![]() ,
,
即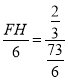 ,
,
∴![]()
②当点![]() 在线段
在线段![]() 上,同理可得
上,同理可得![]()

【题目】为了了解同学们寒假期间每天健身的时间![]() (分),校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表,已知
(分),校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表,已知![]() 组所在扇形的圆心角为
组所在扇形的圆心角为![]() .
.
组别 | 频数统计 |
| 8 |
| 12 |
|
|
| 15 |
| b |
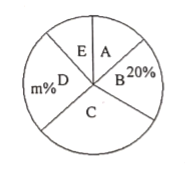
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有 人,![]() ,
,![]() ,
,![]() ;
;
(2)求扇形统计图中扇形![]() 的圆心角度数;
的圆心角度数;
(3)该校共有学生1200人,请估计每天健身时间不少于1小时的人数.