题目内容
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像分别交于点
的图像分别交于点![]() 和点B.
和点B.
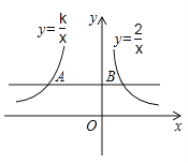
![]() 若
若![]() 线段
线段![]() 的长度是
的长度是![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的值;
的值;
![]() 嘉淇同学观察了三个函数图像后,大胆猜想:“当
嘉淇同学观察了三个函数图像后,大胆猜想:“当![]() 一定时,
一定时,![]() 的面积一定随
的面积一定随![]() 的增大而增大.”你认为他的猜想对吗.说明理由;
的增大而增大.”你认为他的猜想对吗.说明理由;
![]() 在
在![]() 的条件下,若直线
的条件下,若直线![]() 与
与![]() 的图像有交点,与
的图像有交点,与![]() 的图像无交点,请直接写出
的图像无交点,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)A(-6,1),B(2,1),k=﹣6;(2)嘉淇的猜想不对,理由解析;(3)0<n<6
【解析】
(1)把y=1代入![]() 可得点B坐标,由AB=8可得点A坐标,把点A坐标代入
可得点B坐标,由AB=8可得点A坐标,把点A坐标代入![]() 即可求出k;
即可求出k;
(2)当y=m时,分别求出点A、B的坐标,进而可得AB的长,然后即可求出△OAB的面积,从而可判断嘉淇同学的猜想;
(3)由直线![]() 与
与![]() 的图象有交点可得n的一个取值范围,由直线
的图象有交点可得n的一个取值范围,由直线![]() 与
与![]() 的图象无交点可再得n的一个取值范围,取其公共部分即得结果.
的图象无交点可再得n的一个取值范围,取其公共部分即得结果.
解:(1)当m=1时,把y=1代入![]() ,得x=2,
,得x=2,
∴B(2,1),
∵AB=8,
∴A(﹣6,1),
把A(﹣6,1)代入![]() ,
,
∴ k=﹣6![]() 1=﹣6;
1=﹣6;
(2) 把y=m代入![]() ,得
,得![]() ,
,
∴B(![]() ,m),
,m),
把y=m代入![]() ,得
,得![]() ,
,
∴A(![]() ,m),
,m),
∴AB=![]() ﹣
﹣![]() =
=![]() ,
,
∴![]() ,
,
∴△OAB的面积与m无关.
∴嘉淇的猜想不对;
(3)∵直线![]() 与
与![]() 的图象有交点,
的图象有交点,
∴方程![]() 即
即![]() 有两个实数根,
有两个实数根,
∴![]() ,解得:
,解得:![]() 或
或![]() (舍去),
(舍去),
又∵![]() ,∴
,∴![]() ;
;
∵直线![]() 与
与![]() 的图象无交点,
的图象无交点,
∴方程![]() 即
即![]() 没有实数根,
没有实数根,
∴![]() ,解得:0<n<6;
,解得:0<n<6;
综上所述,![]() 的取值范围是:0<n<6.
的取值范围是:0<n<6.

练习册系列答案
相关题目