题目内容
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF.

(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90º,且四边形AECF是菱形,求BE的长.

(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90º,且四边形AECF是菱形,求BE的长.
(1)证明见解析;(2)菱形,5.
试题分析:(1)首先由已知证明AF∥EC,BE=DF,推出四边形AECF是平行四边形.
(2)由已知先证明AE=BE,即BE=AE=CE,从而求出BE的长.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴AF∥EC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形.
(2)解:如图.
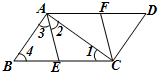
∵四边形AECF是菱形,
∴AE=EC,
∴∠1=∠2,
∵∠3=90°﹣∠2,∠4=90°﹣∠1,
∴∠3=∠4,
∴AE=BE,
∴BE=AE=CE=
 BC=5.
BC=5.考点: 1.平行四边形的判定与性质;2.菱形的性质。

练习册系列答案
相关题目




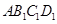 的边长为1,
的边长为1, ;作
;作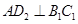 于点
于点 ,以
,以 为一边,做第二个菱形
为一边,做第二个菱形 ,使
,使 ;作
;作 于点
于点 ,以
,以 为一边做第三个菱形
为一边做第三个菱形 ,使
,使 ;
; 依此类推,这样做的第
依此类推,这样做的第 个菱形
个菱形 的边
的边 的长是 .
的长是 .
 ,宽为
,宽为 的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,将剪下的部分打开,得到的菱形的面积为( )
的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,将剪下的部分打开,得到的菱形的面积为( )



