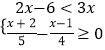题目内容
【题目】问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求![]() 的值.
的值.
(1)初步尝试
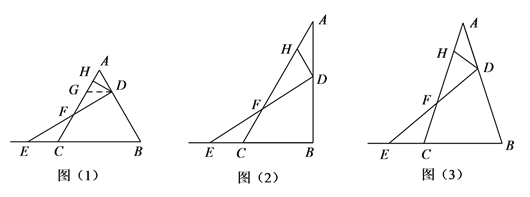
如图(1),若△ABC是等边三角形,DH⊥AC,且点D、E的运动速度相等,小王同学发现可以过点D作DG∥BC交AC于点G,先证GH=AH,再证GF=CF,
从而求得![]() 的值为 .
的值为 .
(2)类比探究
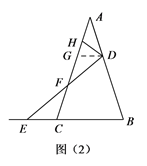
如图(2),若△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是![]() ︰1,求
︰1,求![]() 的值.
的值.
(3)延伸拓展
如图(3)若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记![]() =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示![]() 的值(直接写出果,不必写解答过程).
的值(直接写出果,不必写解答过程).
【答案】(1)2;(2)![]() ;(3)
;(3)![]()
![]()
【解析】(1)过点D作DG∥BC交AC于点G,由题意知△AGD是等边三角形,所以AD=GD,所以可以证明△GDF≌△CEF,所以CF=GF,由三线合一可知:AH=GH,所以![]() =2;
=2;
(2)过点D作DG∥BC交AC于点G,由点D、E的运动速度之比是![]() :1可知GD=CE,所以可以证明△GDF≌△CEF,所以CF=GF,所以CF=GF,由∠ABC=90°,∠ADH=∠BAC=30°可知:AH=DH,所以
:1可知GD=CE,所以可以证明△GDF≌△CEF,所以CF=GF,所以CF=GF,由∠ABC=90°,∠ADH=∠BAC=30°可知:AH=DH,所以![]() =2;
=2;
(3)类似(1)(2)的方法可求出![]() =m和
=m和![]() =m,然后利用GH+FG=m(AC-HF),
=m,然后利用GH+FG=m(AC-HF),
即可求出![]() 的值.
的值.
解:(1)过点D作DG∥BC交AC于点G,
∵△ABC是等边三角形,
∴△AGD是等边三角形,
∴AD=GDA,
由题意知:CE=AD,
∴CE=GD,
∵DG∥BC,
∴∠GDF=∠CEF,
在△GDF与△CEF中,
∠GDF=∠CEF,∠GFD=∠EFC,CE=GD,
∴△GDF≌△CEF(AAS),
∴CF=GF,
∵DH⊥AG,
∴AH=GH,
∴AC=AG+CG=2GH+2CF=2(GH+CF),HF=GH+GF,
∴![]() =2;
=2;
(2)
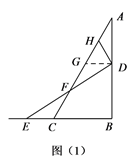
如图(1)过点D作DG∥BC交AC于点G,
则∠ADG=∠ABC=90°.
∵∠BAC=∠ADH=30°,
∴AH=DH,∠GHD=∠BAC+∠ADH=60°,
∠HDG=∠ADG-∠ADH=60°,
∴△DGH为等边三角形.
∴GD=GH =DH =AH,AD=GD·tan60°=![]() GD.
GD.
由题意可知,AD=![]() CE.∴GD=CE.
CE.∴GD=CE.
∵DG∥BC,∴∠GDF=∠CEF,∠DGF=∠ECF.
∴△GDF≌△CEF.∴GF=CF.
GH+GF=AH+CF,即HF=AH+CF,
∴HF=![]() AC=2,即
AC=2,即![]() .
.
(3)![]()
![]() .
.
提示:如图(2)
 ,
,
过点D作DG∥BC交AC于点G,
在△ABC中,∵∠BAC=∠ADH=36°,AB=AC,
∴AH=DH,∠ACB=∠B=72°,∠GHD=∠HAD+∠ADH=72°.
∴∠AGD=∠GHD=72°.
∵∠GHD=∠B=∠HGD=∠ACB,∴△ABC∽△DGH.∴![]() ,
,
∴GH=mD H=mA H.
由△ADG∽△ABC可得![]() .
.
∵DG∥BC,∴![]() .∴FG=mFC.
.∴FG=mFC.
∴GH+FG=m(AH+FC)=m(AC-HF),
即HF=m(AC-HF).∴![]()
![]() .
.
“点睛”本题考查三角形的综合问题,涉及全等三角形的判定和性质,相似三角形的判定与性质,等边三角形的性质,直角三角形的性质等知识,内容比较综合,需要学生灵活运用所学的知识进行解答.