题目内容
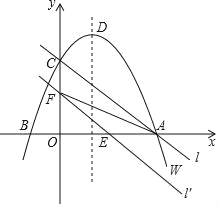
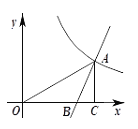
【题目】如图,直线y1=2x-3与双曲线![]() 在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC.
在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC.
(1)求A,B两点的坐标及k的值;
(2)请直接写出当y2>y1>0时x的取值范围.
【答案】(1)k=2;(2)![]() <x<2
<x<2
【解析】试题分析:(1)根据直线与x轴的交点,令y=0,求出点B的坐标,然后根据解直角三角形求出A点的坐标,利用待定系数法求出k的值;
(2)根据函数的图像和交点,直接可写出取值范围.
试题解析:由y1=2x-3=0,解得![]() ,所以B(
,所以B(![]() ,0),OB=
,0),OB=![]() .
.
设点A的横坐标为m(m>0),则纵坐标为2m-3,BC= ![]() ,AC=2m-3,
,AC=2m-3,
∵AC⊥x轴,∴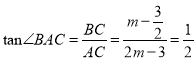 .
.
∵∠BAC=∠AOC,∴ ![]() ,解得m =2,
,解得m =2,
∴2m-3=1,即A(2,1)
把A(2,1)代入![]() ,得
,得![]() ,解得k=2
,解得k=2
(2)![]() <x<2
<x<2

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目