Question

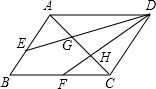如图，已知E、F分别为△ABC的边AB、BC的中点，G、H为AC边上的两个三等分点，连EG、FH，且延长后交于点D，则下列说法正确的是

1. A.
   ∠ABC=∠ADC
2. B.
   EG=FH
3. C.
   DE=DF
4. D.
   ∠ADC=3∠GDH

Answer 1

A
分析：连接BG，BH，先由三角形中位线定理可得HF∥BG，EG∥BH，则四边形FDGB是平行四边形，再利用平行四边形的对角线互相平分可得OB=OD，OH=OG，又AG=CH，所以OA=OC，根据对角线互相平分的四边形是平行四边形，得出四边形ABCH是平行四边形，从而得到∠ABC=∠ADC．即可判定A正确．
解答：解：连接BG、BH．
∵F是BC中点，G、H是AC上的三等分点，
∴BF=FC，GH=HC，
∴FH∥BG．
同理可得，GE∥BH．
∴四边形BHDG是平行四边形．
连接BD，交AC于O，
则BO=DO，GO=HO．
又∵G、H是AC上的三等分点，
∴AG=HC．
∴AG+GO=HC+HO，即AO=CO．
又∵BO=DO，
∴四边形ABCD是平行四边形，
∴∠ABC=∠ADC，A正确．
而根据已知条件无法判定B、C、D正确．
故选A．
点评：本题考查了三角形中位线定理，平行四边形的判定与性质，难度中等，关键是辅助线的作出．