题目内容
 (2013•宜宾)如图:已知D、E分别在AB、AC上,AB=AC,∠B=∠C,求证:BE=CD.
(2013•宜宾)如图:已知D、E分别在AB、AC上,AB=AC,∠B=∠C,求证:BE=CD.分析:要证明BE=CD,把BE与CD分别放在两三角形中,证明两三角形全等即可得到,而证明两三角形全等需要三个条件,题中已知一对边和一对角对应相等,观察图形可得出一对公共角,进而利用ASA可得出三角形ABE与三角形ACD全等,利用全等三角形的对应边相等可得证.
解答:证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=CD(全等三角形的对应边相等).
|
∴△ABE≌△ACD(ASA),
∴BE=CD(全等三角形的对应边相等).
点评:此题考查了全等三角形的判定与性质,全等三角形的判定方法为:SSS;SAS;ASA;AAS;HL(直角三角形判定全等的方法),常常利用三角形的全等来解决线段或角相等的问题,在证明三角形全等时,要注意公共角及公共边,对顶角等隐含条件的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
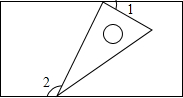 (2013•宜宾)如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2=
(2013•宜宾)如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2=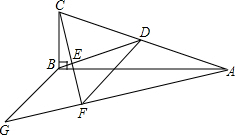 (2013•宜宾)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为
(2013•宜宾)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为 (2013•宜宾)如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足
(2013•宜宾)如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足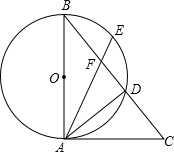 (2013•宜宾)如图,AB是⊙O的直径,∠B=∠CAD.
(2013•宜宾)如图,AB是⊙O的直径,∠B=∠CAD.
 (2013•宜宾)如图,抛物线y1=x2-1交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
(2013•宜宾)如图,抛物线y1=x2-1交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.