题目内容
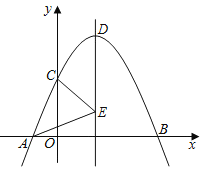
【题目】如图,二次函数y=ax2+bx+c的图象与x轴相交于点A(﹣1,0)、B(5,0),与y轴相交于点C(0,![]() ).
).
(1)求该函数的表达式;
(2)设E为对称轴上一点,连接AE、CE;
①当AE+CE取得最小值时,点E的坐标为 ;
②点P从点A出发,先以1个单位长度/的速度沿线段AE到达点E,再以2个单位长度的速度沿对称轴到达顶点D.当点P到达顶点D所用时间最短时,求出点E的坐标.
【答案】(1)![]() ;(2)①(2,
;(2)①(2,![]() );②点E(2,
);②点E(2,![]() ).
).
【解析】
(1)抛物线的表达式为:y=a(x+1)(x﹣5)=a(x2﹣4x﹣5),故﹣5a=![]() ,解得:a=﹣
,解得:a=﹣![]() ,即可求解;
,即可求解;
(2)①点A关于函数对称轴的对称点为点B,连接CB交函数对称轴于点E,则点E为所求,即可求解;
②t=AE+![]() DE,t=AE+
DE,t=AE+![]() DE=AE+EH,当A、E、H共线时,t最小,即可求解.
DE=AE+EH,当A、E、H共线时,t最小,即可求解.
(1)抛物线的表达式为:y=a(x+1)(x﹣5)=a(x2﹣4x﹣5),
故﹣5a=![]() ,解得:a=﹣
,解得:a=﹣![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)①函数的对称轴为:x=2,
点A关于函数对称轴的对称点为点B,连接CB交函数对称轴于点E,则点E为所求,
由点B、C的坐标得,BC的表达式为:y=﹣![]() x+
x+![]() ,
,
当x=2时,y=![]() ,
,
故答案为:(2,![]() );
);
②t=AE+![]() DE,
DE,
过点D作直线DH,使∠EDH=30°,作HE⊥DH于点H,则HE=![]() DE,
DE,
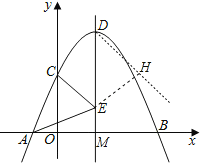
t=AE+![]() DE=AE+EH,当A、E、H共线时,t最小,
DE=AE+EH,当A、E、H共线时,t最小,
则直线A(E)H的倾斜角为:30°,
直线AH的表达式为:y=![]() (x+1)
(x+1)
当x=2时,y=![]() ,
,
故点E(2,![]() ).
).

练习册系列答案
相关题目