题目内容
【题目】如图,四边形ABCD中,∠ADC=∠ABC=90°,与∠ADC、∠ABC相邻的两外角平分线交于点E,若∠A=50°,则∠E的度数为( )

A. 60°B. 50°C. 40°D. 30°
【答案】C
【解析】
运用四边形的内角和等于360°,可求∠DCB的度数,再利用角平分线的性质及三角形的外角性质可求∠E的度数.
解:如图,连接EC并延长,
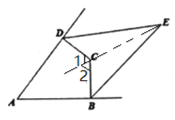
∵∠ADC=∠ABC=90°,∠A=50°,
∴∠DCB=360°-90°-90°-50°=130°,
∵∠ADC、∠ABC相邻的两外角平分线交于点E,
∴∠CDE=∠CBE=45°,
∵∠1=∠CDE+∠DEC,∠2=∠CBE+∠BEC
即∠DCB=∠CDE+∠CBE+∠BED=130°,
∴∠BED=130°-45°-45°=40°.
故选:C.

练习册系列答案
相关题目