题目内容
已知方程4x2-2（m+1）x+m=0的两根恰好是一个直角三角形两锐角的余弦值，则m的值为（ ）A．±
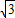
B．
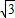
C．-
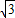
D．不能确定
【答案】分析：设直角三角形的两锐角分别为∠A，∠，根据根与系数的关系表示出两根之和与两根之积，利用同角三角函数间的基本关系变形，再利用完全平方公式化简，得到关于m的方程，求出方程的解即可得到m的值．
解答：解：设直角三角形的两锐角分别为∠A，∠B，
根据题意得：方程4x2-2（m+1）x+m=0的两根为cosA与cosB（sinA=cosB），
∴cosA+cosB=cosA+sinA=-
，cosAsinA=
＞0，
又sin2A+cos2A=1，
∴（cosA+sinA）2-2sinAcosA=
-
=1，
整理得：m2=3，
解得：m=
或m=-
（舍去），
则m的值为
．
故选B
点评：此题考查了一元二次方程根与系数的关系，以及互余两角三角函数的关系，熟练掌握根与系数的关系是解本题的关键．
解答：解：设直角三角形的两锐角分别为∠A，∠B，
根据题意得：方程4x2-2（m+1）x+m=0的两根为cosA与cosB（sinA=cosB），
∴cosA+cosB=cosA+sinA=-
，cosAsinA=＞0，又sin2A+cos2A=1，
∴（cosA+sinA）2-2sinAcosA=
-=1，整理得：m2=3，
解得：m=
或m=-（舍去），则m的值为
．故选B
点评：此题考查了一元二次方程根与系数的关系，以及互余两角三角函数的关系，熟练掌握根与系数的关系是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知方程4x2-3x=0，下列说法正确的是（ ）
A、只有一个根x=
| ||
| B、只有一个根x=0 | ||
C、有两个根x1=0，x2=
| ||
D、有两个根x1=0，x2=-
|
已知方程4x2-mx+5=0的两根为x1=1，x2=
，则二次函数y=4x2-mx+5与x轴的交点坐标为（ ）
| 5 |
| 4 |
| A、（1，0） | ||
B、（1，0），（
| ||
C、（
| ||
| D、（4，0），（5，0） |