题目内容
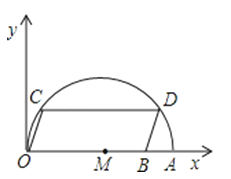
【题目】已知:点M、P、N、Q依次是正方形ABCD的边AB、BC、CD、DA上一点(不与正方形的顶点重合),给出如下结论:
①MN⊥PQ,则MN=PQ;
②MN=PQ,则MN⊥PQ;
③△AMQ≌△CNP,则△BMP≌△DNQ;
④△AMQ∽△CNP,则△BMP∽△DNQ
其中所有正确的结论的序号是 .
【答案】①②③
【解析】解:连接QM,MP,PN,PQ,过N作NE⊥AB于E,过Q作QF⊥BC于F,
则四边形BCNE,四边形CDQF是矩形,
∴EN=BC,QF=CD,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,
∴NE=QF,
①∵MN⊥PQ,
∴∠PQF=∠MNE,
在△PQF与△MNE中, 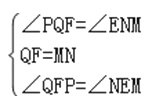 ,
,
∴△PQF≌△MNE,
∴MN=PQ;
②在Rt△PQF与Rt△MNE中, 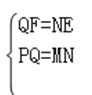 ,
,
∴Rt△PQF≌Rt△MNE,
∴∠PQF=∠MNE,
∵∠PQF+∠1=90°,
∴∠MNE+∠1=90°,
∴MN⊥PQ;
③∵△AMQ≌△CNP,
∴AM=CN,PC=AQ,
∴PB=QD,BM=DN,
在△BMP与△DNQ中, 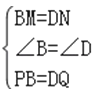 ,
,
∴△BMP≌△DNQ,
④由△AMQ∽△CNP和已知条件推不出△BMP∽△DNQ的条件.
所以答案是:①②③.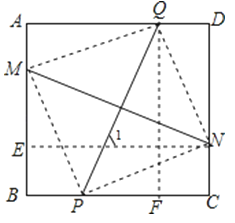

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】![]() 筐葡萄,以每筐
筐葡萄,以每筐![]() 千克为标准,超过或不足的千克数分别用正、负数来表示,与标准质量的差值记录如下:
千克为标准,超过或不足的千克数分别用正、负数来表示,与标准质量的差值记录如下:
单位(千克) |
|
|
|
|
|
|
筐数 |
|
|
|
|
|
|
(1)![]() 筐葡萄中,最重的一筐比最轻的一筐重________千克.
筐葡萄中,最重的一筐比最轻的一筐重________千克.
(2)与标准重量比较,![]() 筐葡萄总计超过或不足多少千克?
筐葡萄总计超过或不足多少千克?
(3)若葡萄每千克售价![]() 元,则出售这
元,则出售这![]() 筐葡萄可卖多少元?
筐葡萄可卖多少元?