题目内容
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标.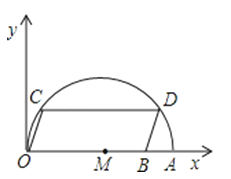
【答案】解:∵四边形OCDB是平行四边形,点B的坐标为(8,0),
CD∥OA,CD=OB=8
过点M作MF⊥CD于F,则CF=![]() CD=4
CD=4
过C作CE⊥OA于E,
∵A(10,0),
∴OA=10,OM=5
∴OE=OM﹣ME=OM﹣CF=5﹣4=1
连接MC,MC=![]() OA=5
OA=5
∴在Rt△CMF中,
MF= ![]() =
=![]() =3
=3
∴点C的坐标为(1,3)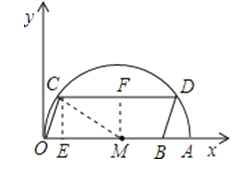
【解析】过点M作MF⊥CD于F,过C作CE⊥OA于E,在Rt△CMF中,根据勾股定理即可求得MF与EM,进而就可求得OE,CE的长,从而求得C的坐标.
【考点精析】本题主要考查了垂径定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某商店能过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:
第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
调整前单价x(元) | x1 | x2=6 | x3=72 | x4 | … | xn |
调整后单价x(元) | y1 | y2=4 | y3=59 | y4 | … | yn |
已知这n个玩具调整后的单价都大于2元.
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为![]() ,
,![]() ,猜想
,猜想![]() 与
与![]() 的关系式,并写出推导出过.
的关系式,并写出推导出过.