题目内容
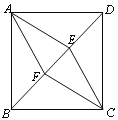
【题目】如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.
⑴求证:四边形AECF是菱形.
⑵若AB=2,BF=1,求四边形AECF的面积.
【答案】(1)证明见解析;
(2)四边形AECF的面积为4﹣2![]() .
.
【解析】试题分析:(1)根据正方形的性质,可得正方形的四条边相等,对角线平分对角,根据 SAS,可得△ABF与△CBF与△CDE与△ADE的关系,根据三角形全等,可得对应边相等,再根据四条边相等的四边形,可得证明结果;
(2)根据正方形的边长、对角线,可得直角三角形,根据勾股定理,可得AC、EF的长,根据菱形的面积公式,可得答案.
试题解析:(1)证明:正方形ABCD中,对角线BD,
∴AB=BC=CD=DA,
∠ABF=∠CBF=∠CDE=∠ADE=45°.
∵BF=DE,
∴△ABF≌△CBF≌△DCE≌△DAE(SAS).
AF=CF=CE=AE
∴四边形AECF是菱形;
(2)∵AB=2,∴AC=BD=![]()
∴OA=OB=![]() =2.
=2.
∵BF=1,
∴OF=OB-BF=2-1.
∴S四边形AECF=![]() ACEF=
ACEF=![]() .
.

练习册系列答案
相关题目