题目内容
(本小题满分14分)
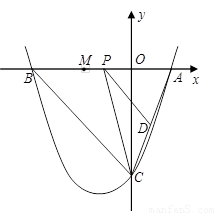
已知:如图,抛物线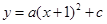 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
(1)求该抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PD∥BC,交AC于点D,连接CP.当△CPD的面积最大时,求点P的坐标;
(3)若平行于x轴的动直线 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(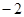 ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 ,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
(1)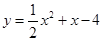
(2)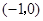
(3) 或
或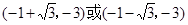
【解析】(1)由题意,得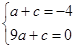
解得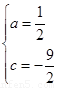 .……2分
.……2分
∴所求抛物线的解析式为: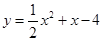 ..……3分
..……3分
(2)设点P的坐标为(x,0),过点D作DG⊥x轴于点G.
∴由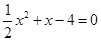 ,得
,得 .
.
∴点A的坐标为(2,0),点B的坐标为(-4,0)..……4分
∴AB=6,BP=2-x.
∵点P在线段AB上,
∴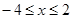 ..……5分
..……5分
∵PD∥BC,
∴△APD∽△ABC
∴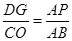
即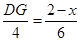 ,∴
,∴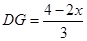 .
.
∴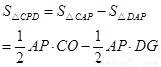
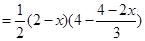
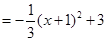 .……8分
.……8分
又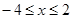 ,
,
∴当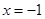 时,
时,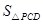 有最大值3,此时P
有最大值3,此时P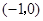 ..……9分
..……9分
(3)存在.
在△OMF中.
①若MO=MF,∵B(-4,0),M(-2,0),故BM=OM=MF=2.
又在Rt△BOC中,OB=OC=4,∴∠OBC=45°.∴∠MFB=∠OBC=45°.
∴∠BMF=90°.此时,点F的坐标为(-2,-2).
由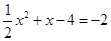 ,得
,得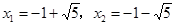 .
.
此时,点Q的坐标为: ..……11分
..……11分
②若OF=MF,过点F作FE⊥x轴于点E,
由等腰三角形的性质得: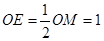 ,∴BE=3,
,∴BE=3,
∴在等腰直角△BEF中,EF=BE=3.∴F(-1,-3).
由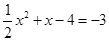 ,得
,得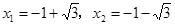 .
.
此时,点Q的坐标为: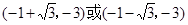 ..……13分
..……13分
③若OM=OF,∵OB=OC=4,且∠BOC=90°,∴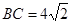 ,
,
∴点O到BC的距离为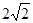 ,而OF=OM=2<
,而OF=OM=2<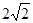 ,
,
此时,不存在这样的直线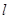 ,使得△OMF是等腰三角形..……14分
,使得△OMF是等腰三角形..……14分
综上所述,存在这样的直线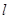 ,使得△OMF是等腰三角形.所求点Q的坐标为:
,使得△OMF是等腰三角形.所求点Q的坐标为:
 或
或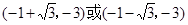 .
.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案 如图13,二次函数
如图13,二次函数 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为( ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线 与抛物线交于点B、C.
与抛物线交于点B、C.
 与
与 的面积。
的面积。 时,
时, 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.