题目内容
(2011广西崇左,25,14分)(本小题满分14分)已知抛物线y=x2+4x+m(m为常数)
经过点(0,4).
(1) 求m的值;
(2) 将该抛物线先向右、再向下平移得到另一条抛物线.已知平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为直线l1)关于y轴对称;它所对应的函数的最小值为-8.
① 试求平移后的抛物线的解析式;
② 试问在平移后的抛物线上是否存在点P,使得以3为半径的圆P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被圆P所截得的弦AB的长度;若不存在,请说明理由.
【答案】
(1)代入(0,4)得m =4;
(2)①平移前对称轴l1为x= - 2,平移后对称轴l2为x= 2,最小值为-8,故抛物线方程为y=(x-2)2-8.
②设P的坐标为(x0,y0),则y0=-3,x0=2±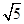 或y0=3,x0=2±
或y0=3,x0=2±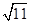
又P到x=2的距离小于3,故x0=2±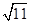 舍去,
舍去,
综上,存在这样的点P,且点P的坐标为(-3,2±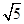 ).
).
【解析】略

练习册系列答案
相关题目


