Question

25.（本小题满分14分）

如图13，二次函数的图象与x轴交于A、B两点，与y轴交于点C（0，-1），ΔABC的面积为。

（1）求该二次函数的关系式；

（2）过y轴上的一点M（0，m）作y轴上午垂线，若该垂线与ΔABC的外接圆有公共点，求m的取值范围；

（3）在该二次函数的图象上是否存在点D，使四边形ABCD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。

Answer 1

解：（1）OC=1,所以,q=-1,又由面积知0.5OC×AB=,得AB=

设A（a,0）,B(b,0)

AB=b-a==，解得p=,但p<0,所以p=。

所以解析式为：

（2）令y=0，解方程得，得,所以A(,0),B(2,0),在直角三角形AOC中可求得AC=,同样可求得BC=,，显然AC²+BC²=AB²,得三角形ABC是直角三角形。AB为斜边，所以外接圆的直径为AB=,所以.

（3）存在，AC⊥BC,①若以AC为底边，则BD//AC,易求AC的解析式为y=-2x-1,可设BD的解析式为y=-2x+b，把B(2,0)代入得BD解析式为y=-2x+4，解方程组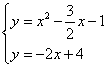得D（,9）

②若以BC为底边，则BC//AD,易求BC的解析式为y=0.5x-1,可设AD的解析式为y=0.5x+b，把 A(,0)代入得AD解析式为y=0.5x+0.25，解方程组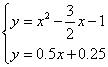得D()

综上，所以存在两点：（,9）或()。