Question

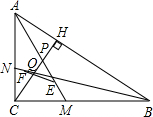已知△ABC中，∠ACB=90°，AB边上的高线CH与△ABC的两条内角平分线AM、BN分别交于P、Q两点，PM、QN的中点分别为E、F，求证：EF∥AB．

Answer 1

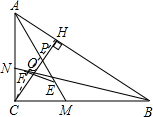证明：连接CF、FH，
∵BN是∠ABC的平分线，
∴∠ABN=∠CBN，
又∵CH⊥AB，
∴∠CQN=∠BQH=90°-∠ABN=90°-∠CBN=∠CNB，
∴CQ=NC．
又F是QN的中点，
∴CF⊥QN，
∴∠CFB=90°=∠CHB，
∴C、F、H、B四点共圆．
又∠FBH=∠FBC，
∴FC=FH，
∴点F在CH的中垂线上，
同理可证，点E在CH的中垂线上，
∴EF⊥CH，
又AB⊥CH，
∴EF∥AB．
分析：连接CF、FH，因为BN平分∠ABC，利用互余关系、对顶角相等可证∠CNB=∠BQH=∠CQN，根据CF为△CQN的底边上中线，可证CF⊥BN，可知∠CFB=90°=∠CHB，由此可证C、F、H、B四点共圆，根据BN平分∠ABC，可证FC=FH，即点F在CH的中垂线上，同理可证，点E在CH的中垂线上，故EF⊥CH，而AB⊥CH，可证EF∥AB．
点评：本题考查了线段垂直平分线的判断，四点共圆的判断与运用．关键是根据题意构造四点共圆的条件．本题具有一定的综合性．