题目内容
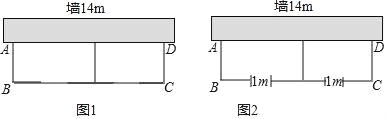
【题目】如图,在直线l上摆放着三个三角形:△ABC、△HFG、△DCE,已知BC=![]() CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
【答案】2 6.
【解析】
根据题意,可以证明S2与S1两个平行四边形的高相等,长是S1的3倍,S3与S2的长相等,高是S3的![]() ,这样就可以把S1和S3用S2来表示,从而计算出S2的值.
,这样就可以把S1和S3用S2来表示,从而计算出S2的值.
根据正三角形的性质,∠ABC=∠HFG=∠DCE=60°,∴AB∥HF∥DC∥GN,设AC与FH交于P,CD与HG交于Q,∴△PFC、△QCG和△NGE是正三角形.
∵F、G分别是BC、CE的中点,∴MF=![]() AC=
AC=![]() BC,PF=
BC,PF=![]() AB=
AB=![]() BC.
BC.
又∵BC=![]() CE=
CE=![]() CG=
CG=![]() GE,∴CP=MF,CQ=
GE,∴CP=MF,CQ=![]() BC=3PF,QG=GC=CQ=
BC=3PF,QG=GC=CQ=![]() AB=3CP,∴S1=
AB=3CP,∴S1=![]() S2,S3=3S2.
S2,S3=3S2.
∵S1+S3=20,∴![]() S2+3S2=20,∴S2=6,∴S1=2.
S2+3S2=20,∴S2=6,∴S1=2.
故答案为:2;6.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为![]() .
.
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.