题目内容
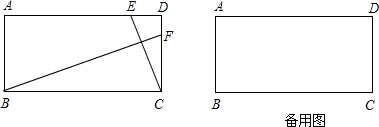
已知在矩形ABCD中,AD>AB,O为对角线的交点,过O作一直线分别交BC、AD于M、N
(1)求证:S梯形ABMN=S梯形CDNM;
(2)当M、N满足什么条件时,将矩形ABCD以MN为折痕翻折后能使C点恰好与A点重合(只写出满足的条件,不要求证明);
(3)在(2)的条件下,若翻折后不重叠部分的面积是重叠部分面积的 ,求
,求 的值.
的值.

 (1)证明:如图(一),连AC、BD交于O,
(1)证明:如图(一),连AC、BD交于O,∵AD∥BC,
∴∠DNM=∠BMN,
∵四边形ABCD是矩形,
∴AB=CD,
∵∠BOM=∠DON,
∴△DON≌△BOM,
∴ND=BM,
同理可证△AON≌△COM,
∴AN=MC,
∴AN+ND=BM+MC,
∵AB=CD,
∴S梯形ABMN=S梯形CDNM;
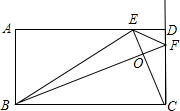
(2)解:如图(二),
∵当A点与C点重合时,△AMO≌△CMO,
∴MN⊥AC,这是MN应满足的条件;
(3)解:如图(二),
∵AB=CD=AD′,
∵∠BAM+∠MAN=90°,∠MAN+∠NAD′=90°,
∴∠BAM=∠NAD′,又∠B=∠D′=90°,
∴△ABM≌△AD′N,
∴△ABM和△AD′N的面积相等,MC=AM=AN,
∵重叠部分是△AMN,不重叠部分是△ABM和△AD′N.
∴
 =
= ,即
,即 =
= ,
,故
 =
= .
.分析:(1)连AC、BD交于O,根据四边形ABCD是矩形可求出△DON≌△BOM,△AON≌△COM,再由梯形的面积即可求解;
(2)根据图形翻折不变性的性质即可解答;
(3)根据图形翻折后不重叠部分的面积是重叠部分面积的
 列出关系式,再把三角形面积的比转化为
列出关系式,再把三角形面积的比转化为 的比即可.
的比即可.点评:本题考查的是图形翻折变换的性质、梯形的面积公式及三角形的面积,熟知以上知识是解答此题的关键.

练习册系列答案
相关题目
 ,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).
,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).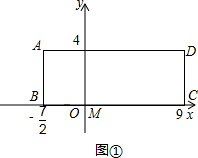
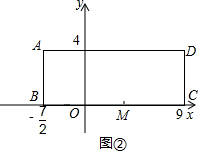
 (2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.
(2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.