题目内容
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的点P坐标;若不存在,请说明理由.
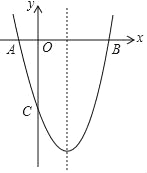
【答案】(1)y=x2﹣2x﹣3;(2)存在,理由见解析;符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ).
).
【解析】
(1)先求出点C的坐标,在由BO=OC=3AO,确定出点B,A的坐标,最后用待定系数法求出抛物线解析式.
2)设出点P的坐标,表示出PB,PC,求出BC,分三种情况利用两边相等建立方程求解即可.
(1)∵抛物线y=ax2+bx﹣3,
∴c=﹣3,
∴C(0,﹣3),
∴OC=3,
∵BO=OC=3AO,
∴BO=3,AO=1,
∴B(3,0),A(﹣1,0),
∵该抛物线与x轴交于A、B两点,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3,
(2)存在,
理由:设P(1,m),
∵B(3,0),C(0,﹣3),
∴BC=3![]() ,PB=
,PB=![]() ,PC=
,PC=![]() ,
,
∵△PBC是等腰三角形,
①当PB=PC时,
∴![]() =
=![]() ,
,
∴m=﹣1,
∴P(1,﹣1),
②当PB=BC时,
∴3![]() =
=![]() ,
,
∴m=±![]() ,
,
∴P(1,![]() )或P(1,﹣
)或P(1,﹣![]() ),
),
③当PC=BC时,
∴3![]() =
=![]() ,
,
∴m=﹣3±![]() ,
,
∴P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ),
),
∴符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ).
).

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目