题目内容
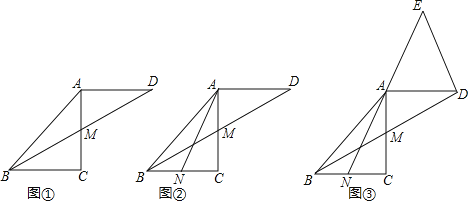
【题目】已知△ABC是等腰直角三角形,∠C=90°,点M是AC的中点,延长BM至点D,使DM=BM,连接AD.
(1)如图①,求证:△DAM≌△BCM;
(2)已知点N是BC的中点,连接AN.
①如图②,求证:△BCM≌△ACN;
②如图③,延长NA至点E,使AE=NA,连接DE.求证:BD⊥DE.
【答案】(1)见解析;(2)①见解析;②见解析.
【解析】
(1)利用SAS进行证明即可;
(2)由点M是AC的中点,点N是BC的中点,AC=BC,可得CM=CN,继而利用SAS进行证明即可;
②取AD中点F,连接EF,则AD=2AF,由△BCM≌△ACN,△DAM≌△BCM,可推导得出AF=CN,∠EAF=∠ANC,根据SAS可证明△EAF≌△ANC,从而可得∠NAC=∠AEF,∠C=∠AFE=90°,进而可得∠AFE=∠DFE=90°,继而可以证明△AFE≌△DFE,则有∠EAD=∠EDA=∠ANC,继而可得∠EDB=90°,问题得证.
(1)∵点M是AC的中点,∴AM=CM,
在△DAM和△BCM中,
∵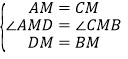 ,∴△DAM≌△BCM(SAS);
,∴△DAM≌△BCM(SAS);
(2)①∵点M是AC的中点,点N是BC的中点,∴CM=![]() AC,CN=
AC,CN=![]() BC,
BC,
∵△ABC是等腰直角三角形,∴AC=BC,∴CM=CN,
在△BCM和△ACN中,∵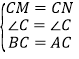 ,∴△BCM≌△ACN(SAS);
,∴△BCM≌△ACN(SAS);
②取AD中点F,连接EF,

则AD=2AF,
∵△BCM≌△ACN,∴AN=BM,∠CBM=∠CAN,
∵△DAM≌△BCM,∴∠CBM=∠ADM,AD=BC=2CN,
∴AF=CN,∴∠DAC=∠C=90°,∠ADM=∠CBM=∠NAC,
∴AD∥BC,∴∠EAF=∠ANC.
在△EAF和△ANC中,∵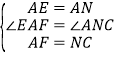 ,∴△EAF≌△ANC(SAS),
,∴△EAF≌△ANC(SAS),
∴∠NAC=∠AEF,∠C=∠AFE=90°,∴∠AFE=∠DFE=90°,
∵F为AD的中点,∴AF=DF,
在△AFE和△DFE中,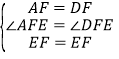 ,
,
∴△AFE≌△DFE(SAS),
∴∠EAD=∠EDA=∠ANC,
∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°–∠DAM=180°–90°=90°,
∴BD⊥DE.

 阅读快车系列答案
阅读快车系列答案