题目内容
【题目】如图所示的折线是某个函数的图象,根据图象解答下列问题.
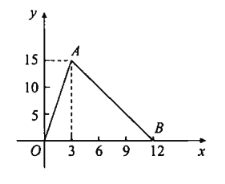
(1)写出自变量x的取值范围:__________,函数值y的取值范围:__________;
(2)求这个分段函数的表达式.
【答案】(1)0≤x≤12;0≤y≤15;(2)y=5x(0≤x≤3),y=![]() x+20(3≤x≤12)
x+20(3≤x≤12)
【解析】
(1)根据函数图象的意义可得出x的取值范围和函数值y的范围;
(2)由图象可求得A、B两点的坐标,利用待定系数法可求出直线AB与OA的解析式.
解:(1)由图象可知自变量x的取值范围为:0≤x≤12,
对应函数值y的取值范围为:0≤y≤15,
(2)由图象得A,B的坐标分别为(3,15),(12,0),![]()
设此一次函数解析式为y=k1x+b1,把A、B两点坐标代入可得![]()
解得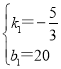
∴直线AB的函数解析式为y=![]() x+20(3≤x≤12)
x+20(3≤x≤12)
设直线OA的函数解析式为y=k2x+b2,把把A、O两点坐标代入可得![]()
解得![]()
∴直线OA的函数解析式为y=5x(0≤x≤3)
故答案为(1)0≤x≤12;0≤y≤15;(2)y=5x(0≤x≤3),y=![]() x+20(3≤x≤12)
x+20(3≤x≤12)

练习册系列答案
相关题目