Question

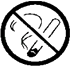
【题目】如图所示，已知：DG⊥BC，AC⊥BC，FE⊥AB，∠1=∠2.

求证：CD⊥AB.

证明：∵DG⊥BC，AC⊥BC(已知)

∴∠DGB=∠ACB=90°(垂直的定义)

∴DG∥AC( )

∴∠2=∠DCA( )

∵∠1=∠2(已知)

∴∠1= (等量代换)

∴ (同位角相等，两直线平行)

∴ =∠ADC( )

∵EF⊥AB(已知)， ∴∠AEF=90°( )，∴∠ADC=90° ，

∴CD⊥AB(垂直的定义)

Answer 1

【答案】见解析.

【解析】

灵活运用垂直的定义，注意由垂直可得90°角，由90°角可得垂直，结合平行线的判定和性质，只要证得∠ADC＝90°，即可得CD⊥AB．

∵DG⊥BC，AC⊥BC(已知)

∴∠DGB=∠ACB=90°(垂直的定义)

∴DG∥AC( 同位角相等，两直线平行 )

∴∠2=∠DCA( 两直线平行，内错角相等 )

∵∠1=∠2(已知)

∴∠1= ∠DCA (等量代换)

∴ EF∥DC (同位角相等，两直线平行)

∴∠AEF =∠ADC( 两直线平行，同位角相等 )

∵EF⊥AB(已知)，

∴∠AEF=90°( 垂直的定义 )，

∴∠ADC=90° ，

∴CD⊥AB(垂直的定义)．