题目内容
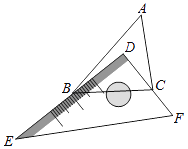
【题目】如图，∠l=∠2，DE⊥BC，AB⊥BC，那么∠A=∠3吗？说明理由．
解：∠A=∠3，理由如下：
∵DE⊥BC，AB⊥BC（已知）
∴∠DEB=∠ABC=90° （ ）
∴∠DEB+（ ）=180°
∴DE∥AB （ ）
∴∠1=∠A（ ）
∠2=∠3（ ）
∵∠l=∠2（已知）
∴∠A=∠3（ ）
【答案】理由见解析.
【解析】分析：先根据垂直定义得到
，则利用平行线的判定可得DE∥AB，然后根据平行线得性质得到∠2=∠3，∠1=∠A，再利用等量代换可得
详解：∵DE⊥BC,AB⊥BC(已知)
∴ (垂直的定义)，
∴
∴DE∥AB(同旁内角互补相等,两直线平行)，
∴∠1=∠A(两直线平行,同位角相等)，
由DE∥BC还可得到：
∠2=∠3(两直线平行,内错角相等)，
又∵∠1=∠2(已知)
∴∠A=∠3(等量代换).
故答案为:垂直的定义；∠ABC；同旁内角互补，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等；等量代换.
练习册系列答案
相关题目
【题目】某校八年级学生在学习《数据的分析》后，进行了检测，现将该校八（1）班学生的成绩统计如下表，并绘制成条形统计图（不完整）． 
分数（分） | 人数（人） |
68 | 4 |
78 | 7 |
80 | 3 |
88 | 5 |
90 | 10 |
96 | 6 |
100 | 5 |
（1）补全条形统计图；
（2）该班学生成绩的平均数为86.85分，写出该班学生成绩的中位数和众数；
（3）该校八年级共有学生500名，估计有多少学生的成绩在96分以上（含96分）？
（4）小明的成绩为88分，他的成绩如何，为什么？